-
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2015 MX2 Marathon ADVANCED (archive) (1 Viewer)
- Thread starter Trebla
- Start date
- Status
- Not open for further replies.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2015 4U Marathon - Advanced Level
Not sure about whether or not you can avoid induction.
I think my method was an induction, but might have involved contradiction in proving one of the steps.Hi seanieg89. I can get some sort of induction argument going, but was wondering if there is a proof by contradiction. It seems just right for one!?
Not sure about whether or not you can avoid induction.
simpleetal
Member
- Joined
- Apr 6, 2015
- Messages
- 54
- Gender
- Male
- HSC
- 2016
Re: HSC 2015 4U Marathon - Advanced Level
sorry but can you explain what the question is asking for? I don't know what that last symbol is supposed to mean.
simpleetal
Member
- Joined
- Apr 6, 2015
- Messages
- 54
- Gender
- Male
- HSC
- 2016
Re: HSC 2015 4U Marathon - Advanced Level
Assuming that the symbol means "for x between and including 0, and 1", I get an integer answer. Is it an integer answer? I'd like post my solution, but only if I'm sure that there's no sillies.
- Joined
- Feb 16, 2005
- Messages
- 8,635
- Gender
- Male
- HSC
- 2006
Re: HSC 2015 4U Marathon - Advanced Level
I think this question is beyond the Ext2 course (the whole idea of convex sets and the intersections of such sets).
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2015 4U Marathon - Advanced Level
Then the second sentence is just asking:
If we have a finite collection of convex sets in the plane such that any three sets from this collection share a common point, then show that there exists a point common to ALL of the sets in this collection.
Do you understand the definition of a convex set in the first sentence?sorry but can you explain what the question is asking for? I don't know what that last symbol is supposed to mean.
Then the second sentence is just asking:
If we have a finite collection of convex sets in the plane such that any three sets from this collection share a common point, then show that there exists a point common to ALL of the sets in this collection.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2015 4U Marathon - Advanced Level
a) The polynomial has real coefficients. (Otherwise any three different complex numbers with the same imaginary part can be non-real roots of a polynomial with positive .)
.)
b) The polynomial has distinct roots. (If any roots have multiplicity > 1, then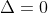 . Still, all roots will be real in this case).
. Still, all roots will be real in this case).
Under these assumptions, we now prove your claim.
The only if is trivial.
Now suppose such a cubic has not all roots real. As non-real roots come in conjugate pairs, we must have roots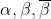 for some real
for some real  and some non-real
and some non-real 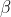 .
.
So
^2(\alpha-\overline{\beta})^2(\beta-\overline{\beta})^2=|\alpha-\beta|^4(2i \textrm{Im}(\beta))^2 < 0.)
So any cubic polynomial with positive must have all roots real and distinct.
must have all roots real and distinct.
Interesting point: The obvious generalisation of this quantity alone doesn't tell us whether the roots are all real if we are talking about higher degree polynomials! (Eg for a quartic, you can have two pairs of conjugate roots, and so two negative terms in with positive product.) A potentially fun challenge problem is to construct a quantity in terms of a monic quartic's coefficients (maybe assume that the ^3 coefficient is zero to simplify the calculations. this can be arranged by a linear substitution anyway) that is positive if and only if it's roots are distinct reals.
with positive product.) A potentially fun challenge problem is to construct a quantity in terms of a monic quartic's coefficients (maybe assume that the ^3 coefficient is zero to simplify the calculations. this can be arranged by a linear substitution anyway) that is positive if and only if it's roots are distinct reals.
This is only necessarily true if:
a) The polynomial has real coefficients. (Otherwise any three different complex numbers with the same imaginary part can be non-real roots of a polynomial with positive
b) The polynomial has distinct roots. (If any roots have multiplicity > 1, then
Under these assumptions, we now prove your claim.
The only if is trivial.
Now suppose such a cubic has not all roots real. As non-real roots come in conjugate pairs, we must have roots
So
So any cubic polynomial with positive
Interesting point: The obvious generalisation of this quantity alone doesn't tell us whether the roots are all real if we are talking about higher degree polynomials! (Eg for a quartic, you can have two pairs of conjugate roots, and so two negative terms in
Last edited:
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2015 4U Marathon - Advanced Level
,y_2=f(1/2),y_3=f(1).)
(Note that the evaluation at any three points uniquely determines a polynomial of degree <= 2, and that the conditions of the question imply that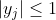 ).
).
Solving the resulting simultaneous equations gives a,b,c in terms of the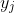 .
.
We get
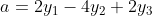
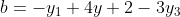
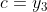
Now the triangle inequality tells us
+ 2(|y_3|+|y_2|)\leq 8)
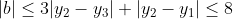
So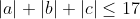 , and we can obtain equality with
, and we can obtain equality with 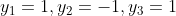 , that is
, that is 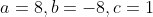 for example.
for example.
Let
(Note that the evaluation at any three points uniquely determines a polynomial of degree <= 2, and that the conditions of the question imply that
Solving the resulting simultaneous equations gives a,b,c in terms of the
We get
Now the triangle inequality tells us
So
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2015 4U Marathon - Advanced Level
) be the claim for a given positive integer
be the claim for a given positive integer 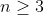 .
.
Let's assume that we know) and
and ) for some
for some 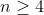 .
.
Then we will show that) is true.
is true.
To see this, let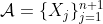 be such a collection of convex sets.
be such a collection of convex sets.
Then write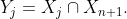 As the intersection of two convex sets is convex (I can write a separate proof for this if its not obvious enough for me to assume), we have that
As the intersection of two convex sets is convex (I can write a separate proof for this if its not obvious enough for me to assume), we have that 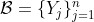 is a collection of convex sets.
is a collection of convex sets.
Moreover, for any distinct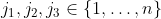 , we have
, we have 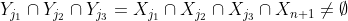
where the last inequality follows from) and our assumption that every triple of sets from
and our assumption that every triple of sets from 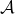 has a common element.
has a common element.
In other words we have shown that every triple of sets from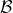 has a common point.
has a common point.
From) we conclude that
we conclude that 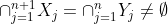 , which is precisely the statement
, which is precisely the statement ) .
.
This reduces the problem to proving) , which can be tackled geometrically. I will do this in a separate post now to make the whole proof more readable.
, which can be tackled geometrically. I will do this in a separate post now to make the whole proof more readable.
Okay, so let
Let's assume that we know
Then we will show that
To see this, let
Then write
Moreover, for any distinct
where the last inequality follows from
In other words we have shown that every triple of sets from
From
This reduces the problem to proving
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2015 4U Marathon - Advanced Level
Suppose) were not true.
were not true.
Then given such convex sets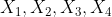 , we could find distinct points in the plane
, we could find distinct points in the plane 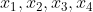 such that
such that 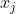 is only in the three sets that AREN'T
is only in the three sets that AREN'T 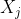 .
.
But any four points in the plane define a unique convex quadrilateral Q.
Without loss of generality suppose this quadrilateral has vertices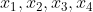 in anti-clockwise order.
in anti-clockwise order.
Then by convexity, the diagonal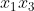 lies in
lies in 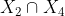 and the diagonal
and the diagonal 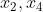 lies in
lies in 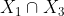 .
.
As the diagonals of a convex quadrilateral intersect, that means the point of intersection of these diagonals must lie in every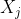 .
.
This completes the proof of) , and hence the whole problem.
, and hence the whole problem.
Suppose
Then given such convex sets
But any four points in the plane define a unique convex quadrilateral Q.
Without loss of generality suppose this quadrilateral has vertices
Then by convexity, the diagonal
As the diagonals of a convex quadrilateral intersect, that means the point of intersection of these diagonals must lie in every
This completes the proof of
Re: HSC 2015 4U Marathon - Advanced Level
Can you post a problem which you found to be quite tough from when you were year 12?Supposewere not true.
Then given such convex sets, we could find distinct points in the plane
such that
is only in the three sets that AREN'T
.
But any four points in the plane define a unique convex quadrilateral Q.
Without loss of generality suppose this quadrilateral has verticesin anti-clockwise order.
Then by convexity, the diagonallies in
and the diagonal
lies in
.
As the diagonals of a convex quadrilateral intersect, that means the point of intersection of these diagonals must lie in every.
This completes the proof of, and hence the whole problem.
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2015 4U Marathon - Advanced Level
I can't really remember off the top of my head. Try some of the problems from olympiads.Can you post a problem which you found to be quite tough from when you were year 12?
simpleetal
Member
- Joined
- Apr 6, 2015
- Messages
- 54
- Gender
- Male
- HSC
- 2016
Re: HSC 2015 4U Marathon - Advanced Level
^{(n+1)} +(-n)^n $ [text\]{is congruent to}$ (k+1)^{k+1} +(-k)^k mod 9 $where k = 0--> 8.$ $ $testing manually for k = 0 to 8 shows that the expression is not 0 mod 9 for any such k, and thus $ (n+1)^{(n+1)}$ $+ (-n)^n $is not divisble by 9 for any natural number n.$ )
Prove that (n+1)^(n+1) + (-n)^n is not divisble by 9 for any natural number n.
Last edited:
RealiseNothing
what is that?It is Cowpea
Re: HSC 2015 4U Marathon - Advanced Level
Define a function by:
 = m)
Where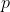 is prime,
is prime,  is real, and
is real, and  is the highest integer power of
is the highest integer power of 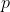 that divides
that divides  .
.
Note that doesn't have to be integer. i.e.
doesn't have to be integer. i.e.  = f_2(2^{\frac{1}{3}} \times 5^{\frac{1}{3}}) = \frac{1}{3})
You are given that the function defined has the property that:
 = f_k(p) - f_k(q))
Use this function to prove that the square root of all non-square positive integers is irrational.
Define a function by:
Where
Note that
You are given that the function defined has the property that:
Use this function to prove that the square root of all non-square positive integers is irrational.
Last edited:
Re: HSC 2015 4U Marathon - Advanced Level
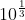 ? Didn't you say
? Didn't you say  needed to be integer?
needed to be integer?
How can we have the example ofDefine a function by:
Whereis prime,
is a positive integer, and
is the highest power of
that divides
.
Note thatdoesn't have to be integer. i.e.
You are given that the function defined has t
he property that:
Use this function to prove that the square root of all non-square positive integers is irrational.
Last edited:
- Status
- Not open for further replies.
