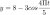HSC 2015 MX1 Marathon (archive) (1 Viewer)

Sy123 · Jun 27, 2015

Re: HSC 2015 3U Marathon

davidgoes4wce said:
Find the coefficient of x^2 in (x+(1/x))^3 (x+1)^5

i get an answer of 55 but the solution says 92.0

Neither of those are correct:

http://www.wolframalpha.com/input/?i=(x+1/x)^3+(1+x)^5

$\left(x + \frac{1}{x} \right)^3 (1+x)^5 = \frac{1}{x^3} (1+x^2)^3(1+x)^5$

$\\ $So, instead of finding the coefficient of$ \ x^2 \ $we can find the coefficient of$ \ x^5 \ $in$ \\ (1+x^2)^3 (1+x)^5 \ $since it becomes divided by the$ \ x^3 \ $in front$$

$\\ $Coefficeint of $\ x^5 \ $in$ \ \underbrace{(1+x^2)^3}_{A} \underbrace{(1+x)^5}_B \ $can be gotten by $ \\ $(1): multiplying a constant from$ \ A \ $and a$ \ x^5 \ $in B$ \\ \\ $There are no odd power terms in$ \ A \ $so the next case is$ \\ $(2): multiplying a$ \ x^2 \ $from$ \ A \ $and a$ \ x^3 \ $from B.$ \\ $(3): Multiplying a$ \ x^4 \ $from$ \ A \ $and a$ \ x \ $from B$$

$\\ $Therefore the coefficient is$ \ \binom{3}{0} \cdot \binom{5}{5} x^5 + \binom{3}{1} (x^2) \cdot \binom{5}{3} x^3 + \binom{3}{2} (x^2)^2 \cdot \binom{5}{1} x \\ \\ = x^5 \left(\binom{3}{0} \binom{5}{5} + \binom{3}{1} \binom{5}{3} + \binom{3}{2} \binom{5}{1} \right) = 46x^2 \\ \\ $Therefore the coefficient is$ \ 46$

(as per the expansion)

davidgoes4wce · Jun 27, 2015

Re: HSC 2015 3U Marathon

THanks for the reply, I did get 46 by doing the long expansion

leehuan · Jun 29, 2015

Re: HSC 2015 3U Marathon

$Prove that $\left( \begin{matrix} n+1 \\ k+1 \end{matrix} \right) =\left( \begin{matrix} n \\ k \end{matrix} \right) +\left( \begin{matrix} n \\ k+1 \end{matrix} \right) \\ $1. By the definition of the binomial coefficient.$ \\ $2. Using a binomial expansion.$ \\ \\ $Explain why the result holds true with reference to Pascal's Triangle and combinations.$

davidgoes4wce · Jun 30, 2015

Re: HSC 2015 3U Marathon

[URL=http://s571.photobucket.com/user/Tran_David/media/Screen_Shot_2015-06-30_at_3_zpseefwe0c0.jpg.html]

[/URL]

Can someone explain to me why the answer is 17 and why it couldn't also be -17?

davidgoes4wce · Jun 30, 2015

Re: HSC 2015 3U Marathon

Also can someone give me a better way to do a square root on LaTeX?

InteGrand · Jun 30, 2015

Re: HSC 2015 3U Marathon

davidgoes4wce said:
[URL=http://s571.photobucket.com/user/Tran_David/media/Screen_Shot_2015-06-30_at_3_zpseefwe0c0.jpg.html][/URL]

Can someone explain to me why the answer is 17 and why it couldn't also be -17?

Basically, the acceleration is positive when it is at x = 6, and its velocity is also positive there, so it starts moving to the right with increasing velocity, and the more it moves to the right, the greater its acceleration becomes (since $\ddot{x}=x$ (given)), and hence its velocity must also become greater. So basically as time goes on, its displacement, velocity, and acceleration are all increasing. By the time it is at x = 15, its velocity must be positive because it must be greater than what it was at x = 6, and the velocity here was positive.

InteGrand · Jun 30, 2015

Re: HSC 2015 3U Marathon

davidgoes4wce said:
Also can someone give me a better way to do a square root on LaTeX?

Square root of x say would be written with this code: \sqrt{x} (\sqrt is for square root, then put what you want under the square root in curly brackets). The result looks like this: $\sqrt{x}$ .

davidgoes4wce · Jun 30, 2015

Re: HSC 2015 3U Marathon

I was using the \surd{x} notation, thanks for clearing that up

Sy123 · Jun 30, 2015

Re: HSC 2015 3U Marathon

Drsoccerball · Jun 30, 2015

Re: HSC 2015 3U Marathon

Sy123 said:

$\binom{13}{4}(p)^4(1-p)^9 = 3 \cdot \binom{13}{3}p^3(1-p)^{10}$

$$ Rearranging $ p=\frac{6}{11}$

davidgoes4wce · Jul 2, 2015

Re: HSC 2015 3U Marathon

This question is from J.P Kinny-Lewis, is there a problem with the question

The rise and fall of the tide is assumed to be simple harmonic, with the time between successive high tides being 12.5 hours. In the entrance of a certain harbour the depth of water at high tide is 11 m and at low tide 5 m. On a certain day low tide occurs at 5am.

i) SHow that the water depth, y metres, at the entrance is given by

[/URL][/IMG]

I got y=8- 3 cos (4 PI t/25)

Crisium · Jul 2, 2015

Re: HSC 2015 3U Marathon

davidgoes4wce said:
This question is from J.P Kinny-Lewis, is there a problem with the question

The rise and fall of the tide is assumed to be simple harmonic, with the time between successive high tides being 12.5 hours. In the entrance of a certain harbour the depth of water at high tide is 11 m and at low tide 5 m. On a certain day low tide occurs at 5am.

i) SHow that the water depth, y metres, at the entrance is given by

[/URL][/IMG]

I got y=8- 3 cos (4 PI t/5)

Assuming you mean that you got y = 8 - 3cos (4pi t / 25)

Centre of motion: 8 (Mid point between high and low tide (11 + 5) / 2 = 8)

Amplitude: 3 (Distance from high/low tide to the centre of motion (8 - 5 = 3 or 11 - 8 = 3)

Value of n:

Using the period formula period = 2pi / n

They say that the time between successive high tides is 12.5 hours which is the period.

12.5 = 2pi / n

Rearranging you get

n = 2pi / 12.5

Multiply the numerator and denominator by two to get whole numbers

n = 4pi / 25

The standard form of this equation would be

y = B - Acos(nt)

Therefore

y = 8 - 3cos (4pi t / 25)

ALWAYS draw a diagram to establish whether it is sin or cos, and whether it is positive or negative.

EDIT:

It is a negative cos graph.

There is a low tide at 5 AM - take that as time zero (i.e. When the graph begins) and when you sub in t = 0 you get 5 m which is the low tide value.

Crisium · Jul 2, 2015

Re: HSC 2015 3U Marathon

Apologies for the dodgy working out / guide on answering the question, I can't LaTex like all you pros :3

davidgoes4wce · Jul 2, 2015

Re: HSC 2015 3U Marathon

The answer in J.P Kinny Lewis has y=8- 3 cos (4 pi t/25) so I definitely think the 'original question' was wrong

they say to use x= a cos (nt + b) + c

davidgoes4wce · Jul 2, 2015

Re: HSC 2015 3U Marathon

Inverse Functions also taken from the J.P Kinny Lewis textbook

Can someone confirm for me that we have to use the domain values in order to determine the range.

In this case we have to sub x=0 and x=1 to determine the range. My initial thinking and the way I determined the range in the past was simply to multiply by 3 (the number in front of 3 cos )

davidgoes4wce · Jul 2, 2015

Re: HSC 2015 3U Marathon

This was the question

InteGrand · Jul 2, 2015

Re: HSC 2015 3U Marathon

Multiplying the range of $y= \cos ^{-1}x$ by 3 would also have given you the right range. The reason they evaluated the function at the endpoints was that it would give them two more points on the curve, so it would make it easier to sketch the curve, as they now have three points that the curve go through (as they obtained one in part (i)).

It is a good idea for these sketching of inverse trig. functions questions to obtain key points on the graph before sketching it.

davidgoes4wce · Jul 2, 2015

Re: HSC 2015 3U Marathon

davidgoes4wce said:
Inverse Functions also taken from the J.P Kinny Lewis textbook

Can someone confirm for me that we have to use the domain values in order to determine the range.

In this case we have to sub x=0 and x=1 to determine the range. My initial thinking and the way I determined the range in the past was simply to multiply by 3 (the number in front of 3 cos )

my other question with this graph now Im assuming that because of the '1-2x' part of this function, the graph is an 'increasing ' function going from left to right?

InteGrand · Jul 2, 2015

Re: HSC 2015 3U Marathon

davidgoes4wce said:
my other question with this graph now Im assuming that because of the '1-2x' part of this function, the graph is an 'increasing ' function going from left to right?

Yes, because of the negative coefficient of the x, the graph is essentially flipped about the vertical axis compared to the orientation of $y=\cos ^{-1}x$ .

davidgoes4wce · Jul 2, 2015

Re: HSC 2015 3U Marathon

Curious to also know has a 'First Principles' question ever popped up in previous years' exam papers for MX1? 3 unit?

One of the students who I chat to says that their school has not covered it and the teachers have not put it into their school curriculum

Make a Difference – Donate to Bored of Studies!

HSC 2015 MX1 Marathon (archive) (1 Viewer)

This too shall pass

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

This too shall pass

Well-Known Member

Well-Known Member

Attachments

Pew Pew

Pew Pew

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Users Who Are Viewing This Thread (Users: 0, Guests: 1)