yes I know that much... but it goes against the orbital velocity equation which is why I started this thread...
The probe needs to gain potential energy to get into an orbit of larger radius.
So, the orbital velocity equation only applies when it is in a stable orbit? When the speed is first halved in the question, the orbit is no longer stable, equation no longer applies.. hence it undergoes orbital decay until the KE it gains from losing GPE puts it back into a stable orbit, at which time the equation will apply again?
Think of it like this. You just decreased the speed of the probe. Now there are a few things that can arise from this.
Is the probe obtaining potential energy? No.
So what exactly is going on here? We have a decrease in speed. This means a decrease in kinetic energy.
The relationship
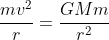
is referring to when the kinetic energy of the probe and potential energy are equal, giving a stable orbit. The relationship you are referring to comes from a derivation using this thought. Hence, you can't apply it to this situation as the rockets have slowed down the probe. However, the kinetic energy has decreased due to the decrease in kinetic energy. If there is a decrease in kinetic energy, then you have to determine the radius r which will allow for a stable orbit. This is where you will find the radius at which there will be a stable orbit.
However, there was no increase in energy applied to the probe. So the probe will not obtain a stable orbit, as the condition for the stable orbit is with a larger radius of orbit.

