isn't it just change in kinetic energy = change in gpe, and also doesnt work done = gpe?
since W=Fs=mgh=Ep (subbing the gravity formula for g)
Work done to get it up into the orbital radius would not be 'mgh', because we can't assume g is constant for larger
r (technically it isn't constant for small
r either, but its variation is negligible for small
r, which is why we assume its constant for things like projectile motion, as it greatly simplifies calculations and produces answers that are suitable for any practical purpose).
If we (the spacecraft) start at
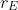
(Earth radius), and go to some radius of orbit

, where r > r
E, then the work done against gravity to go there is given by the following integral:
\text{ d}x\right |$, where $\bold{F}(x)$ is the gravitational force when you are $x$ units from the Earth's centre) $)


= GmM\left(\frac{1}{r_E}-\frac{1}{r} \right)$$)
 \to \frac{GmM}{r_E}$, which is the $GPE$ at the Earth's radius, which is to be expected, as this is how $GPE$ is defined (the work done by gravity to move you from an infinitely far away point to a given distance $r$ from earth)$.)
, so $v^2 = \frac{GM}{r}$. Hence the required $KE$ for orbit at $r$ is $\frac{1}{2}mv^2 =\frac{GmM}{2r}$. This work must be done on the spacecraft to give it the right velocity for orbit (assuming it starts at rest). So the total work done, $W_T$, is$)
 = GmM\left(\frac{1}{r_E}-\frac{1}{r} \right) + \frac{GmM}{2r}$$)
 = GmM\left(\frac{1}{r_E}-\frac{1}{2r} \right)$.$)