Re: HSC 2015 4U Marathon - Advanced Level
If
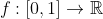
is a non-negative function such that
=1)
and
\geq f(x)+f(y)\quad \textrm{for }0\leq x,y\textrm{ and }x+y\leq 1)
we say that f is a sexy function.
Find the smallest real
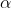
such that
\leq \alpha x)
for all

and all sexy functions
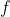
.
It has been a while, so I will post my solution.
I think the answer is
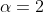
.
First, we show that
\leq 2x)
for all x and all f. (1)
This inequality is certainly true in the interval
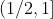
by monotonicity and the fact that f(1)=1.
We now proceed inductively by considering the interval

If the inequality is true in
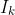
, then for
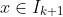
we have
\leq \frac{f(2x)}{2}\leq \frac{4x}{2}=2x)
as

This completes the proof of (1), it remains to show that 2 is the least such constant. We do this by constructing sexy functions which have
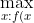\neq 0}\frac{f(x)}{x})
arbitrarily close to 2.
Convexity is the key here, take a function f that satisfies:
i. f(0)=0, f(1)=1.
ii. f is convex on [0,1/2].
iii. f(x)+f(1-x)=1 (symmetry about x=1/2)
I claim that all such functions are sexy. (2)
Note that the function that is 0 on [0,1/2-s], 1 on [1/2+s,1] and (x-1/2)/s on (1/2-s,1/2+s) for some small s clearly satisfies the three above properties. Since it also has f(1/2+s)/(1/2+s)=1/(1/2+s) -> 2, proving (2) would complete the proof that

Let us now prove (2).
Case A:
If x,y,x+y =< 1/2, then f(x+y) >= f(x) + f(y) as f is a convex function on the interval [0,1,2], and convexity implies sexiness as discussed in previous posts.
Case B:
If x,y =< 1/2 and x+y > 1/2, then f(x) + f(y) =< x + y =< f(x)+f(y) where the first inequality is from f(0)=0, f(1/2)=1/2 and convexity in between. The latter inequality is from f(1/2)=1/2, f(1)=1 and concavity in between. (Concavity in this interval following from the symmetry condition iii).
Case C:
If x =< 1/2, and 1 >= y, x+y >1/2, then Case A tells us that f(1-x-y) + f(x) =< f(1-y). Using iii we get 1-f(x+y)+f(x) =< 1-f(y), which gives us sexiness by rearrangement.
This completes the proof of (2), and hence finishes the problem.
$)
+f(x_2)=f(\frac{2 x_1 x_2}{x_1+x_2}))





