Re: HSC 2015 4U Marathon - Advanced Level
While this thread has been bumped, I might as well answer this question because it is pretty cool.
Basically the idea is that we are doing something that in spirit is very much like calculus but on sequences rather than on functions.
If u(n) is a sequence defined on the natural numbers, then we denote it's sequence of differences (the analogue of derivative) by (Du(n):=u(n+1)-u(n)).
We denote it's summation (the analogue of integral) by
:=\sum_{j=0}^n u(j))
Just like in calculus, these two operations are pretty much inverses to each other. We have (SDu)(n)=u(n+1)-u(0) and (DSu)(n)=u(n+1).
This question is then basically asking us to show that all sequences u that solve the equation
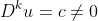
are polynomial sequences of degree k. Induction is clearly the way to go, and the base case of k=0 is trivial.
Supposing then that we have the result for taking < k differences, solving the equation
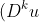(n)=c)
is the same as solving the equation
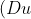(n)=p(n))
where p is a polynomial of degree k-1. By rescaling, we might as well assume p is monic.
The claim is that this latter equation has a polynomial solution of degree k. It is clear that solutions, if they exist, are unique up to constants (again notice the parallels with differentiation and differential equations.)
Now let
=n^m/m.)
By direct computation
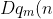=((n+1)^m-n^m)/m=\frac{1}{m}\sum_{k=0}^{m-1} \binom{m}{k}n^k)
is a polynomial of degree m-1.
This means that
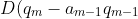)
is a monic polynomial of degree m-1 with m-2 coefficient matching that of p, for a suitable choice of constant
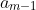
. Continuing this process of subtracting constant multiples of the lower order
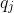
to successively match the coefficients of p we end up with a polynomial q of degree m which solves Dq=p. (Writing this out fully is a basic induction.)
By our earlier remark on uniqueness, this completes the proof.


