Apologies for vagueness, didn't want to hand-hold too much as I think it is a nice thing for a student to discover by him/herself. I will elaborate now

.
Yep, Integrand is exactly right. I was referring to the upper and lower bounds coming from the alternating partial Taylor sums.
That knowing anything about Taylor series is out of syllabus is irrelevant, as you don't need to have seen these before and you don't need to know what these things are called.
It is MX2 knowledge that
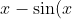\geq 0)
for non-negative real x.
This implies that
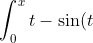\, dt = x^2/2 -1 +\cos(x) \geq 0)
for non-negative real x.
This implies that
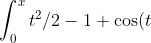 \, dt=x^3/6-x+\sin(x) \geq 0)
for non-negative real x.
etc.
The inequalities arising from iterating this process are exactly those I was referring to with my statement about repeated integration.
Note that combining the above inequalities with what we already know from syllabus, we have:
 \leq x)
for non-negative x, and
 \leq 1.)
We can obtain "tighter" upper and lower bounds for sin and cos by iterating this process. I leave it to you guys to figure out exactly how far you need to go.
Also, as a slight aside: I am sure most of you realise from syllabus knowledge that quantities like sin(cx)/x and sin(cx)/sin(x) tend to c as x tends to zero. For this reason, when we write something like sin(cx)/x in this question, you might as well assume that we are instead referring to the function f(x) that is equal to sin(cx)/x for nonzero x and has f(c)=c. f is continuous at 0 so it is more convenient notationally to do this.
 \sqrt{x^2 + 2}} \, $d$x = \int_{\sqrt{2}}^{\sqrt{3}} \frac{v\text{d}v}{(v^2+1)|v|} = \int_{\sqrt{2}}^{\sqrt{3}} \frac{\text{d}v}{v^2+1} \because \, v>0 \\ \int_0^1 \frac{x}{(x^2 + 3) \sqrt{x^2 + 2}} \, $d$x = \frac{\pi}{3}-\tan^{-1}\sqrt{2})


