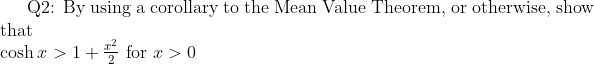Re: MATH1131 help thread
\in \mathbb R^4$ and the plane $\\ \mathcal P =\left\{\textbf{x} \in \mathbb R^4: \textbf{x} = \begin{pmatrix}2\\1\\1\\0\end{pmatrix} + \lambda \begin{pmatrix}0\\3\\-1\\0\end{pmatrix}+ \mu \begin{pmatrix} 0\\1\\3\\0 \end{pmatrix} \right\})
 Find a parametric vector equation of the plane which goes through the point $A$ and is parallel to the plane $\mathcal P)
Easy enough. The answer to this is just
x=(1,0,-1,2)
T+lambda
1(0,3,-1,0)
T+lambda
2(0,1,3,0)
T
 Find a parametric vector equation of a plane which goes though the point $A$, does not intersect $\mathcal P$ and is not parallel to $\mathcal P)
Bit confused as to how to do this question properly. I randomly guessed this one:
x=(1,0,-1,2)
T+mu
1(0,0,-1,0)
T+mu
2(0,1,3,0)
T
Note that the first component of every vector in plane P is 2. So one way to guarantee we don't intersect with P is to make sure vectors in our new plane never have first component 2. And one way to do this is to make the first component of both direction vectors 0, which is what you did, so that's good. (I assume you can see why this ensures the planes won't intersect.)
For the non-parallelism part, note that the span of the direction vectors for P is like "R^2" with first and last component 0. I.e. It is {(0,x,y,0): x, y are real}. This is essentially because the first and last components of the direction vectors in P are both 0 (which is why their span has this property too), and the middle two components (components 2 and 3), if treated like two-tuples, form a basis for R^2. This means in summary that the span of the two direction vectors in P is precisely all vectors of the form (0,x,y,0).
We want our new plane to NOT have this span (since we want non-parallelism). Unfortunately, the direction vectors you chose have exactly the same span as before (so the two planes ARE parallel)! This is because the direction vectors you chose for your proposed plane have first and last component 0 and (0,-1) and (1,3) (the two middle two-tuples in your proposed plane's direction vectors) still span R^2. (I assume you can see why they do this.)
So instead an easy way to prevent the parallelism is to just make one of your current proposed direction vectors have non-zero fourth component (we want 0 first components to ensure first component in proposed plane never has value 2, thus guaranteeing non-intersection with P). So just change your first direction vector in the proposed plane to (0,0,-1,1) say (many possible choices).
Then with this choice of first direction vector (and same second one, which again could be many things), we have ensured the spans of the two planes are different. (Why? Because second plane has (0,0,-1,1) in the span of its direction vectors, which isn't in the first plane's one since this has 1 in its fourth component.)
=x^2+\cosh{(x-1)}+y^3+y)
 Find the equation of the tangent line to the curve $\phi (x,y)=4$ at the point $P(1,1))
 Find $\nabla \phi (1,1)$ and show that it is normal to the tangent line.$)