-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Higher Level Integration Marathon & Questions (1 Viewer)
- Thread starter leehuan
- Start date
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
According to LeehuanSo is this integral from an IB maths textbook?
Re: Extracurricular Integration Marathon
What techniques of integration do they learn in IB? Do they learn Complex Analysis methods? I'm guessing they'd do double integrals?According to Leehuan
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
The classical semicircular contour indented at the origin works for every power series term (Jordan's Lemma) but the problem still remains at bay: How do we justify interchange of summation and integration?We are in the extracurricular marathon, so post a contour integration solution if you do find one.
The slow decay of the integrand again makes things nontrivial (what contour do you suggest?), and the singularity is removable, not a pole so there is no benefit in contouring about it (for the original function, it is a pole of the complexified function, but the problem of slow decay remains).
Re: Extracurricular Integration Marathon
Is Quizlet an online thing, or paper-based?Haven't gotten a proper answer but right now he said some challenge question from "Quizlet"
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Re: Extracurricular Integration Marathon
Turns out it was an...appIs Quizlet an online thing, or paper-based?
Re: Extracurricular Integration Marathon
Nice. So it's not actually IB-related?Turns out it was an...app
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Re: Extracurricular Integration Marathon
My assumption is that it was tagged as an IB challenge question. (That's what he implied at least)Nice. So it's not actually IB-related?
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
Without invoking the Dilogarithm, or using infinite sums of power series, evaluate
}}{x+1}$d$x)
Without invoking the Dilogarithm, or using infinite sums of power series, evaluate
Last edited:
Mongoose528
Member
Re: Extracurricular Integration Marathon
Is this a year 12 topic?
Is this a year 12 topic?
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
No, the Dilogarithm is beyond the curriculum, as is practically everything else on this thread.Is this a year 12 topic?
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Re: Extracurricular Integration Marathon
Integration is a topic in Year 12, however the extent to which it goes is not massive. Even the MX2 Integration Marathon tends to feature questions that are beyond what's examinable in the HSC, let alone the stuff here.Is this a year 12 topic?
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
Here's an easier one. Fun Exercise

Here's an easier one. Fun Exercise
Paradoxica
-insert title here-
Extracurricular Integration Marathon
Also something about the Zeta Regularisation technique.
Fourier expansion. Is that less dodgy, or more?There has to be a less potentially dodgy way of doing it, I also thought of expanding out a series in e^(ix) to start with, but I couldn't see any way of justifying that so I left it.
Gotta be careful with these things, because functions/sequences that oscillate and decay but are not absolutely integrable are a common source of counterexamples to otherwise believable claims.
Also something about the Zeta Regularisation technique.
Last edited:
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: Extracurricular Integration Marathon
Well a power series in e^(ix) IS a Fourier series. The difficulty is in getting a mode of convergence that allows us to commute the limit with the conditionally convergent integral. I did think of an idea that probably deals with it though, and will post it during an afternoon break today if it works.Fourier expansion. Is that less dodgy, or more?
Also something about the Zeta Regularisation technique.
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
Find this limit:
\ln x)
Hence, evaluate this:
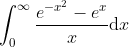
Find this limit:
Hence, evaluate this:
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
A fairly easy exercise.
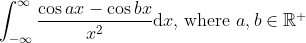
A fairly easy exercise.
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
http://community.boredofstudies.org...ricular-integration-marathon.html#post7092858
But the thing is the justification...
Well the thing I was looking at for Zeta Regularisation was to use the method I used back in the early days of this threadWell a power series in e^(ix) IS a Fourier series. The difficulty is in getting a mode of convergence that allows us to commute the limit with the conditionally convergent integral. I did think of an idea that probably deals with it though, and will post it during an afternoon break today if it works.
http://community.boredofstudies.org...ricular-integration-marathon.html#post7092858
But the thing is the justification...
