projectile question (1 Viewer)
- Thread starter trecex1
- Start date
View attachment 33364
Just need help with part iv) (don't really know what question means) you can assume all other parts are true.
trecex1
Active Member
- Joined
- Mar 19, 2016
- Messages
- 196
- Gender
- Male
- HSC
- 2017
Ok, not sure if solution is basically your method or not, they just moved everything in i) to one side assumed any point (x,y) with 2 solutions then showed product of roots was >1, next step was one of the roots had to be greater than 1. So angle had to be greater than pi/4 for 2 solutions... How did they go from if product of 2 roots (tan(theta)) is >1 that either root has to be >1? If you could explain this or give a simpler solution would be great - seems a lot of work for 1 mark!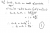 <--- their solution
<--- their solution
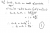 <--- their solution
<--- their solutionAh yeah, that solution is much nicer.Ok, not sure if solution is basically your method or not, they just moved everything in i) to one side assumed any point (x,y) with 2 solutions then showed product of roots was >1, next step was one of the roots had to be greater than 1. So angle had to be greater than pi/4 for 2 solutions... How did they go from if product of 2 roots (tan(theta)) is >1 that either root has to be >1? If you could explain this or give a simpler solution would be great - seems a lot of work for 1 mark!View attachment 33365 <--- their solution
The product of roots is greater than 1. Since the roots are each positive numbers (as they are tan of something that is acute), at least one of them must be greater than 1 (otherwise both would be less than 1, and then their product would have been less than 1 instead of greater than 1. This is because the product of two numbers smaller than 1 is smaller than 1.).
trecex1
Active Member
- Joined
- Mar 19, 2016
- Messages
- 196
- Gender
- Male
- HSC
- 2017
Oh i see, thanks Integrand, would not have thought of this in an exam lol.Ah yeah, that solution is much nicer.
The product of roots is greater than 1. Since the roots are each positive numbers (as they are tan of something that is acute), at least one of them must be greater than 1 (otherwise both would be less than 1, and then their product would have been less than 1 instead of greater than 1. This is because the product of two numbers smaller than 1 is smaller than 1.).

