ProdigyInspired
Tafe Advocate
- Joined
- Oct 25, 2014
- Messages
- 643
- Gender
- Male
- HSC
- 2016
So, as most Ext 2 students know, the last part of Integration involves proving the odd and even definite function proofs.
So for the odd proof (<s>I'll just do it below </s>, its completely wrong don't follow)
<s>
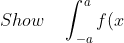 } dx\quad =\quad 0)
 } (-du) \\ =\quad -\int _{ -a }^{ a }{ f(u) } (du) \end{matrix})
Then I get stuck here.
 } =-\int _{ 0 }^{ a }{ f(x) } ) </s>
</s>
I've done it before but I still can't wrap my head around the concept of the dummy variable of x.
If the area is bound by a curve that uses the value of x i.e. f(x), why would it be the same thing as using a variable of f(u)?
So for the odd proof (<s>I'll just do it below </s>, its completely wrong don't follow)
<s>
Then I get stuck here.
I've done it before but I still can't wrap my head around the concept of the dummy variable of x.
If the area is bound by a curve that uses the value of x i.e. f(x), why would it be the same thing as using a variable of f(u)?
Last edited:
