-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2016 MX2 Marathon (archive) (1 Viewer)
- Thread starter Trebla
- Start date
- Status
- Not open for further replies.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2016 4U Marathon
Three mathematics students were seated around a table each wearing a coloured hat, either red or yellow, given to them by their teacher. The students could not see the colour of their own hat, but could see the colour of the other students. The teacher told the students that at least one among them have a yellow hat. The teacher then said that the first student to rise and mention the colour of their own hat would win a prize.
One student finally rose and correctly announced their answer, what did the student say, and how did they work it out?
Three mathematics students were seated around a table each wearing a coloured hat, either red or yellow, given to them by their teacher. The students could not see the colour of their own hat, but could see the colour of the other students. The teacher told the students that at least one among them have a yellow hat. The teacher then said that the first student to rise and mention the colour of their own hat would win a prize.
One student finally rose and correctly announced their answer, what did the student say, and how did they work it out?
kashkow
Active Member
Re: HSC 2016 4U Marathon
The three cases are as follows:
Y-Y-R
Y-R-R
Y-Y-Y
For the sake of the explanation let's name the order of hat wearers as A-B-C respectively.
Case 1: Student A guesses yellow because he thinks that if he has a red hat, student B would immediately deduce he is Yellow. However due to Student B's silence, he must be Yellow.
Case 2: Student A easily deduces he is yellow due to the teachers comment that one must have a yellow hat.
Case 3: Student A can deduce the fact he has a yellow hat, due to the logic of case 1. Assuming the students are all equally rational and logical beings (ie. assuming Student B and C can just as easily come to the same conclusions as A in case 1): If Student A wore a red hat, Students B and C would be able to deduce they are wearing yellow hats. However due to their silence, Student A must be wearing a yellow hat.
Nice question, not too hard. But is this even 4U?? haha shouldn't it be in a logic thread or something?
Edit: P.S. I know a few questions like these (well I can remember one but forgot the specifics other). But I won't post the one I do know for two reasons. 1: not here (don't think this is the appropriate thread?? ahaha) and 2. because it would probably be too easy to solve after this one's been said.
In all cases the answer is Yellow (by any student wearing a yellow hat).Three mathematics students were seated around a table each wearing a coloured hat, either red or yellow, given to them by their teacher. The students could not see the colour of their own hat, but could see the colour of the other students. The teacher told the students that at least one among them have a yellow hat. The teacher then said that the first student to rise and mention the colour of their own hat would win a prize.
One student finally rose and correctly announced their answer, what did the student say, and how did they work it out?
The three cases are as follows:
Y-Y-R
Y-R-R
Y-Y-Y
For the sake of the explanation let's name the order of hat wearers as A-B-C respectively.
Case 1: Student A guesses yellow because he thinks that if he has a red hat, student B would immediately deduce he is Yellow. However due to Student B's silence, he must be Yellow.
Case 2: Student A easily deduces he is yellow due to the teachers comment that one must have a yellow hat.
Case 3: Student A can deduce the fact he has a yellow hat, due to the logic of case 1. Assuming the students are all equally rational and logical beings (ie. assuming Student B and C can just as easily come to the same conclusions as A in case 1): If Student A wore a red hat, Students B and C would be able to deduce they are wearing yellow hats. However due to their silence, Student A must be wearing a yellow hat.
Nice question, not too hard. But is this even 4U?? haha shouldn't it be in a logic thread or something?
Edit: P.S. I know a few questions like these (well I can remember one but forgot the specifics other). But I won't post the one I do know for two reasons. 1: not here (don't think this is the appropriate thread?? ahaha) and 2. because it would probably be too easy to solve after this one's been said.
Last edited:
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2016 4U Marathon
The return of Sy123.
The return of Sy123.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2016 4U Marathon
You've got it. I should of probably of posted it in the advanced thread, having a separate logic thread is going to separate everything too much.In all cases the answer is Yellow (by any student wearing a yellow hat).
The three cases are as follows:
Y-Y-R
Y-R-R
Y-Y-Y
For the sake of the explanation let's name the order of hat wearers as A-B-C respectively.
Case 1: Student A guesses yellow because he thinks that if he has a red hat, student B would immediately deduce he is Yellow. However due to Student B's silence, he must be Yellow.
Case 2: Student A easily deduces he is yellow due to the teachers comment that one must have a yellow hat.
Case 3: Student A can deduce the fact he has a yellow hat, due to the logic of case 1. Assuming the students are all equally rational and logical beings (ie. assuming Student B and C can just as easily come to the same conclusions as A in case 1): If Student A wore a red hat, Students B and C would be able to deduce they are wearing yellow hats. However due to their silence, Student A must be wearing a yellow hat.
Nice question, not too hard. But is this even 4U?? haha shouldn't it be in a logic thread or something?
Edit: P.S. I know a few questions like these (well I can remember one but forgot the specifics other). But I won't post the one I do know for two reasons. 1: not here (don't think this is the appropriate thread?? ahaha) and 2. because it would probably be too easy to solve after this one's been said.
Paradoxica
-insert title here-
Re: HSC 2016 4U Marathon
I created a logic marathon for a reason.
M8You've got it. I should of probably of posted it in the advanced thread, having a separate logic thread is going to separate everything too much.
I created a logic marathon for a reason.
Paradoxica
-insert title here-
Re: HSC 2016 4U Marathon
 = 2\int_0^\frac{\pi}{2} \sin^{2p-1}{x}\cos^{2q-1}{x} \text{d}x )
Clearly, p = n+1 and q = ½ for the integral above.
 = \frac{\Gamma (n+1) \Gamma \left( \frac{1}{2} \right) }{\Gamma \left( n+\frac{3}{2} \right) })
Using Legendre's Duplication Formula:
 \Gamma \left( z+\frac{1}{2} \right) = 2^{1-2z} \Gamma \left( \frac{1}{2} \right) \Gamma (2z))
Set z = n+1
 \Gamma \left( n+\frac{3}{2} \right) = 2^{-(2n+1)} \Gamma \left( \frac{1}{2} \right) \Gamma (2n+2))
Now we can proceed
 = \frac{2^{2n+1} \left( \Gamma \left( n+1 \right) \right)^2 \Gamma \left( \frac{1}{2} \right)}{\Gamma \left( \frac{1}{2} \right) \Gamma \left( 2n+2 \right)} = \frac{2^{2n+1} (n!)^2}{(2n+1)!} = \frac{2^{2n+1}}{(2n+1) \binom{2n}{n}})
Thus we conclude:
 \binom{2n}{n}})
Moving things around we obtain:
\sin^{2n+1}x}{2^{2n}} \text{d}x)
Using the fact that sinx≤1 for all real x, an inequality on the integral is obtained.
\sin^{2n+1}x}{2^{2n}} \text{d}x < \int_0^\frac{\pi}{2} \frac{2n+1}{2^{2n}} \text{d}x = \frac{(2n+1)\pi}{2^{2n+1}})
And hence:
\pi}{2^{2n+1}} = \frac{10\pi}{9})
Thus, by the comparison test, the sum converges absolutely, since all the terms are strictly decreasing and non-negative, with strict upper and lower bounds.
Hence, the interchange of the order of summation and integration is allowed.
\frac{\sin^{2n+1}{x}}{2^{2n}})
\sin^{2n+3}{x}}{2^{2n+2}} - \frac{(2n+1)\sin^{2n+3}{x}}{2^{2n+2}} \right))
 = \sin{x} + \sum_{k=0}^\infty \frac{\sin^{2n+3}{x}}{2^{2n+1}} = \sin{x} + \frac{2\sin^3{x}}{4-\sin^2{x}})
^2})
Integrating across the bounds is a trivial task, and the relevant working will be left as an exercise to the reader.
Thus we conclude:
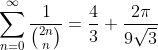
Using the Beta and Gamma Functions we can find an explicit closed form for the integral.
Clearly, p = n+1 and q = ½ for the integral above.
Using Legendre's Duplication Formula:
Set z = n+1
Now we can proceed
Thus we conclude:
Moving things around we obtain:
Using the fact that sinx≤1 for all real x, an inequality on the integral is obtained.
And hence:
Thus, by the comparison test, the sum converges absolutely, since all the terms are strictly decreasing and non-negative, with strict upper and lower bounds.
Hence, the interchange of the order of summation and integration is allowed.
Integrating across the bounds is a trivial task, and the relevant working will be left as an exercise to the reader.
Thus we conclude:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2016 4U Marathon
 \ $d$x \ $for integers$ \ n \geq 0 \\\\ $i) Show that$ \ I_n = \frac{2n}{2n+1}I_{n-1} \ $using integration by parts$ \\\\ $ii) Hence show that$ \ \frac{1}{\binom{2n}{n}} = \frac{2n+1}{4^n}I_n )
 Explain why the infinite sum$ \ \sum_{n=0}^{\infty} (2n+1)z^{2n+1} \ $defined for$ \ |z| < 1 \ $can be written as$ \ \sum_{n=0}^{\infty} (2n+1)z^{2n+1} = \frac{z}{1-z^2} + \frac{2z^3}{1-z^2} + \frac{2z^5}{1-z^2} + \frac{2z^7}{1-z^2} + \dots \\\\ $iv) Hence show that$ \ \sum_{n=0}^{\infty} (2n+1)z^{2n+1} = \frac{z(1+z^2)}{(1-z^2)^2} )
 Now by using part (ii) show that$ \ \sum_{n=0}^{\infty} \frac{1}{\binom{2n}{n}} = 4 \int_0^{\pi /2} \frac{\sin x (4 + \sin^2x)}{(4 -\sin^2 x)^2} \ $d$x \\\\ $vi) Show that$ \ \int \frac{1}{(1+x^2)^2} \ dx = \frac{1}{2} \left(\frac{x}{x^2+1} + \tan^{-1}x \right) + c \\\\ $vii) Evaluate the integral in part (v) using the substitution$ \ u = \cos x \\\\ $viii) Hence show that$ \ \sum_{n=0}^{\infty} \frac{1}{\binom{2n}{n}} = \frac{2}{27}(18 + \pi \sqrt{3}) )
Mostly just algebra and following instructions, it is a fine exercise
EDIT: Will rework so it fits into the non-advanced marathon
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2016 4U Marathon
See my expanded question for a more 4U approachUsing the Beta and Gamma Functions we can find an explicit closed form for the integral.
Clearly, p = n+1 and q = ½ for the integral above.
Using Legendre's Duplication Formula:
Set z = n+1
Now we can proceed
Thus we conclude:
Moving things around we obtain:
Using the fact that sinx≤1 for all real x, an inequality on the integral is obtained.
And hence:
Thus, by the comparison test, the sum converges absolutely, since all the terms are strictly decreasing and non-negative, with strict upper and lower bounds.
Hence, the interchange of the order of summation and integration is allowed.
Integrating across the bounds is a trivial task, and the relevant working will be left as an exercise to the reader.
Thus we conclude:
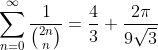
Paradoxica
-insert title here-
Re: HSC 2016 4U Marathon

You didn't formally justify the interchange of summation and integration, so nahSee my expanded question for a more 4U approach
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2016 4U Marathon
Bump, and another question (suitable for this thread):
KingOfActing
lukewarm mess
Re: HSC 2016 4U Marathon
}}{\sin^2{x}} = \lim_{x\to 0} \frac{\sin{(x^2)}}{x^2}\left( \frac{x}{\sin{x}}\right )^2 = 1 \times 1 = 1)
Honestly, I'd consider that 3U level Unless by "With Proof" you meant "By squeeze theorem" in which case I wouldn't see it as a suitable 4u question without more guidance.
Unless by "With Proof" you meant "By squeeze theorem" in which case I wouldn't see it as a suitable 4u question without more guidance.
 Then for $n+1$ we have:$\\\begin{align*}2^{n+3} + 3^{2n+3} &= 2\times 2^{n+2} + 9\times3^{2n+1} \\&=2\times2^{n+2} +2 \times 3^{2n+1} + 7 \times 3^{2n+1} \\&= 7(2m + 3^{2n+1})\end{align*})
Bump, and another question (suitable for this thread):
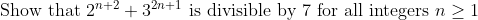
Honestly, I'd consider that 3U level
Last edited:
Paradoxica
-insert title here-
Re: HSC 2016 4U Marathon
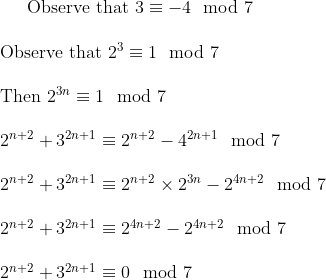
∎
please stop flooding the marathonBump, and another question (suitable for this thread):
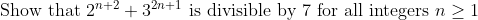
∎
Paradoxica
-insert title here-
Re: HSC 2016 4U Marathon
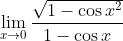
Yeah. Needs to be something harder, like this:}}{\sin^2{x}} = \lim_{x\to 0} \frac{\sin{(x^2)}}{x^2}\left( \frac{x}{\sin{x}}\right )^2 = 1 \times 1 = 1)
Honestly, I'd consider that 3U levelUnless by "With Proof" you meant "By squeeze theorem" in which case I wouldn't see it as a suitable 4u question without more guidance.
Last edited:
Paradoxica
-insert title here-
Re: HSC 2016 4U Marathon
Clearly, these points are reflected about the line y=x, due to the condition on the sum of the angular parameters.
So obviously, the midpoint of the Auxiliary points is the line y=x, inside the auxiliary circle.
Reverse the dilation on the points to bring them back onto the ellipse. Perpendicular dilation from a line does not change the fact that the locus of the midpoints is a line, so the statement is true.
Consider the conjugate points dilated by a constant factor perpendicular to the major axis of the ellipse onto the auxiliary circle which exists alongside the ellipse.
Clearly, these points are reflected about the line y=x, due to the condition on the sum of the angular parameters.
So obviously, the midpoint of the Auxiliary points is the line y=x, inside the auxiliary circle.
Reverse the dilation on the points to bring them back onto the ellipse. Perpendicular dilation from a line does not change the fact that the locus of the midpoints is a line, so the statement is true.
Last edited:
DatAtarLyfe
Booty Connoisseur
- Joined
- Mar 10, 2015
- Messages
- 1,801
- Gender
- Female
- HSC
- 2016
Re: HSC 2016 4U Marathon
so cos(npi/6) = 0
if you solve, you realise that npi/6 = +-(pi/2, 3pi/2, 5pi/2.....) = pi/2 + kpi
Converting to mod-arg form and expanding by DMT, you then make the real part = 0For what values of n is
a) (root(3)+i)^n purely imaginary
Im confused about the npi/6=pi/2 + kpi part. I thought the general solution was 2kpi(plusminus)pi/2?
so cos(npi/6) = 0
if you solve, you realise that npi/6 = +-(pi/2, 3pi/2, 5pi/2.....) = pi/2 + kpi
Re: HSC 2016 4U Marathon

For what values of n is
a) (root(3)+i)^n purely imaginary
Im confused about the npi/6=pi/2 + kpi part. I thought the general solution was 2kpi(plusminus)pi/2?
- Status
- Not open for further replies.
