-
Best of luck to the class of 2024 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
roots help (1 Viewer)
- Thread starter sssona09
- Start date
This is a fourth degree polynomial, so it has four roots. Three of those are identical, so there is only one other unique root.
Firstly, express the polynomial as a product of its factors.
(note that the polynomial is monic, so we may write)
instead of )
)
^3(x-\beta) )
Because these two expressions are identically equal, you may differentiate both sides.
Firstly, express the polynomial as a product of its factors.
(note that the polynomial is monic, so we may write
Because these two expressions are identically equal, you may differentiate both sides.
Last edited:
I differentiate both sides and apply P'(x)=P''(x)=0 ?This is a fourth degree polynomial, so it has four roots. Three of those are identical, so there is only one other unique root.
Firstly, express the polynomial as a product of its factors.
(note that the polynomial is monic, so we may write
Because these two expressions are identically equal, you may differentiate both sides.
Here's another way to do it.
Taking the second derivative of both sides (this is easy for the RHS if you keep factoring out)
^2 + (4x-3\beta-\alpha)2(x-\alpha) \\ 6(2x^2-5x-3) & \equiv 6(x-\alpha)(2x-\alpha-\beta)\end{aligned})
Factorising the LHS,
(2x+1) & \equiv 6(x-\alpha)(2x-\alpha-\beta))
Equating both sides gives us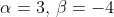
.
____________________________________________________________
Substituting back into the original, we get
Solving,
____________________________________________________________
Alternatively, because this is a monic polynomial, the constant is the product of all the roots, so
We can then solve for
simply by substituting 
into the original polynomial
Taking the second derivative of both sides (this is easy for the RHS if you keep factoring out
Factorising the LHS,
Equating both sides gives us
____________________________________________________________
Substituting back into the original, we get
Solving,
____________________________________________________________
Alternatively, because this is a monic polynomial, the constant is the product of all the roots, so
We can then solve for
Last edited:
I'm pretty sure we can't find differentiate it 2 times since that's a 4U theorem, especially since this is a 3U question, markers may not acknowledge it. It may be faster but I wouldn't risk it. I'll try work out something that doesn't involve that
FINALLY, TOOK ME FOREVER
Sum of roots:
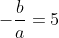
Sum of pairs:
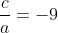
Since the polynomial is monic and we are given it has a triple root
^3(x-\beta))
Therefore we can make two new equations:
$\\\beta=5-3\alpha \\ 3\alpha^2+3\alpha\beta=-9 $ (sum of pairs)$ \\ \end{aligned})
Substitute and expand:
=9\\-6\alpha+15\alpha=-9\\-6\alpha^2+15\alpha+9=0\\2\alpha^2-5\alpha-3=0\end{aligned})
Factorising:
(2\alpha+1)=0\\\alpha=3,-\frac{1}{2}\end{aligned})
Check:
+\beta=5 \\ \beta=\frac{13}{2}\end{aligned})
Therefore, false
+\beta=5\\\beta=-4\end{aligned})
Therefore,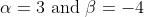
Sum of triplets:
^3+3(3)^2(-4)]=81)
Product of roots:
^3(-4)=-108)
Sum of roots:
Sum of pairs:
Since the polynomial is monic and we are given it has a triple root
Therefore we can make two new equations:
Substitute and expand:
Factorising:
Check:
Therefore, false
Therefore,
Sum of triplets:
Product of roots:
Last edited:
You mean the multiple root theorem?
It's related to my method (from the observation that the triple root
Also, as a side note I've heard that 4U content is accepted in 3U for full marks (and vice versa for 3U and 2U), but the only caveat is that an error means a zero, since the working out is not "valid". If you prove the content before using it I think it's okay though.
Last edited:
Uhhh... guys, can you check this out?
http://m.wolframalpha.com/input/?i=expand+(x+1/2)^3(x-13/2)
http://m.wolframalpha.com/input/?i=expand+(x-3)^3(x+4)
There are 2 solutions both with triple roots
http://m.wolframalpha.com/input/?i=expand+(x+1/2)^3(x-13/2)
http://m.wolframalpha.com/input/?i=expand+(x-3)^3(x+4)
There are 2 solutions both with triple roots
I made an error on this line.
Swapping around the factors on the RHS actually yields another solution:
Since the question didn't say that the coefficients had to be integers, this is also a valid solution. Very interesting... I didn't consider the possibility that two sets of solutions existed.
Last edited:
Yeah man, I thought there was only one solution because the question subtly implied it, I got two solutions then looked at everyone else’s and was like, yeah, I’m probably being dumb so I also took one solution, I happened to be rethinking about the question after school so I brought it up again. lol sorryI made an error on this line.
Swapping around the factors on the RHS actually yields another solution:
Since the question didn't say that the coefficients had to be integers, this is also a valid solution. Very interesting... I didn't consider the possibility that two sets of solutions existed.