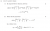Help on Past Paper questions (2 Viewers)

[Skuxxgolfer]

I have been doing past papers from the coroneos extension 2 book and I have trouble understanding some of the solutions they provide, as it isnt set out nicely. So if someone could just briefly outline the solution to these questions, that would be really helpful.
2001: 7bi 8biii and iv
2002: 8aii

 

[lolzdj]

i've only just started the course so i can't really help you, but it seems you're more likely to get a response if you provide screenshots of the questions.

 

[greetings]

Here's the x=p/q one if it helps

 

[greetings]

cot^2(kpi/(2m+1)) question
However, I am unsure whether it is necessary to show x=cot^2(kpi/(2m+1)) is not a solution to p'(x) hence no multiple roots for p(x) meaning p(x) has m distinct roots

 

[InteGrand]

I have been doing past papers from the coroneos extension 2 book and I have trouble understanding some of the solutions they provide, as it isnt set out nicely. So if someone could just briefly outline the solution to these questions, that would be really helpful.
2001: 7bi 8biii and iv
2002: 8aii

Q7(b)(i) is a special case of the rational root theorem. For a proof of this, you can see https://en.wikipedia.org/wiki/Rational_root_theorem#Proofs.

 

[TheOnePheeph]

For 7bi, my method is slightly different to the other posted, but plug x=p/q into the polynomial equation. Doing so and rearranging gives the result:



This means that, since all the numbers present are integers, p divides bq^3. But p and q are coprime (p does not divide q) meaning this can only happen if p divides b. A similar argument can be made rearranging for the ap^3 term. This is essentially proving a case of the rational root theorem, which is for some reason not explicitly taught in 4u.

For 8biii), if we plug r=p/q into the expression, we get:



Now we have two cases to consider. If aq = -bp, then the expression clearly equals 0. Otherwise, however, we know that a,q,b and p are integers, so as long as the expression aq+bp does not equal 0, it will also be an integer. Since all non zero integers have an absolute value greater than or equal to 1:



This means that the given expression is greater than or equal to 1/q.

For 8b iv), we simply consider parts 1 and 2 to show that:



Note, we have assume e=p/q, for coprime p and q, so let a=3q.



But this contradicts the result proved in part iii for rational numbers. Therefore, e must be irrational.

 

[InteGrand]

cot^2(kpi/(2m+1)) question
However, I am unsure whether it is necessary to show x=cot^2(kpi/(2m+1)) is not a solution to p'(x) hence no multiple roots for p(x) meaning p(x) has m distinct roots

 

[Skuxxgolfer]

Thanks for the help people