I think there's a possibility that there's some algebraic trick you can do (independent of the previous parts) to find
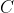
once you know that it actually exists.
Part v) specifically states that the limit exists (with a DO NOT PROVE attached). That would be unnecessary and possibly misleading if the squeeze theorem was intended to be used, as it proves the existence of the limit anyway. I also suspect that the inequality in part i) might be too loose to use the squeeze theorem on.
It looks like parts i) to iv) is a proof that the limit exists using the monotone convergence theorem, with some parts omitted (as the theorem isn't 4U knowledge).

