First, the lack of circle geometry in the MX2 syllabus is a design flaw given the number of complex number problems that are most naturally viewed from that perspective. I don't see how an MX2 student can be well-prepared for MX2 MCQ and complex number sketching without learning some basic circle geometry theorems.
Secondly, I like the approach but I think it is incomplete. Nav123 writes that we "essentially have to prove
}=\arg{\left(\frac{1}{z_3}-\frac{1}{z_2}\right)})
as the two vectors must have the same direction. However, unless I am missing something, this does not necessarily have to be true. We need the points
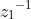
,
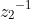
, and
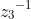
to be collinear.
If 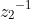
lies between
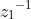
and
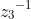 then
then Nav123's goal is sufficient to prove that the points are collinear as the two vectors must point in the same direction and therefore must lie on a single line as they share a common point... but, do the reciprocals have to lie along the common line ordered so that
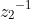
is between the others? I don't see why that is necessarily the case, and if
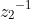
does not lie between
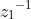
and
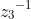
then the arguments of the stated vectors must differ by an odd multiple of
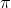
and the principal arguments must be opposite. In that case, we would need to prove
} + \arg{\left(\frac{1}{z_3}-\frac{1}{z_2}\right)} = 0)
or an equivalent statement, such as that
} = \arg{\left(\frac{1}{z_2}-\frac{1}{z_3}\right)})
as we know that the direction to
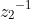
must be the same from
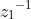
and
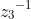
.
A complete proof would either need to cover all possibilities (by taking cases), or it must be set up in such a way that the placement of the three points on the circle (relative to the origin) allows it to be know which reciprocal will be in the centre of the line, but doing so without any loss of generality. Without any preamble being included, this seems to me to be a problem where drawing the diagram can lead to an unnoticed assumption being made and thus restricting the proof to dealing only with a single case. Or am I missing something?
Thirdly, what do others think about how such answers would be taken in school assessments and the HSC. They certainly are valid, but I can see an argument that credit should be restricted when invoking theory not covered in the course, unless a proof of the result being invoked is included. Put another way, I can't see any grounds for less than full marks for a valid proof that invokes a theorem from outside the syllabus and proves that theorem is true as part of the answer. But, what if the result is simply asserted? Assuming there is nothing in the question to prevent its use (like "by using method X", etc). How would HSC markers see that? Schools are free to take their own perspectives, but what do we think those might be? Thoughts? Thanks.


