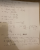-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
inequality (1 Viewer)
- Thread starter s97127
- Start date
pikachu975
Premium Member
This is probably gonna be a dumb question but what's the symbol on the LHS, e.g. (something - a^2)?
(1-a^2)/(1+a^2) + (1-b^2)/(1+b^2) + 2/sqrt(1+c^2) <= 2*sqrt(2)This is probably gonna be a dumb question but what's the symbol on the LHS, e.g. (something - a^2)?
I am not certain that the last part of this is valid.Importantly, because, this explicit formula for
shows that
and thus
.
Therefore the inequality is equivalent to
Finally,
^2(1)^2}{(1+0^2)(1+0^2)} + \frac{1+1}{\sqrt{(1+0^2)(1+0^2)}} = \sqrt 2.)
I agree that we have
must be non-zero:
Similar reasoning allows us to conclude that
satisfies
And, while it may be true that
Consider some values:
Case 1: Both near zero
Case 2: Both near one
Case 3: Both near middle
Case 4: One near zero, one near one
Looking at these four cases, we see that
My bad, I didn't check that last step correctly.
This may not quite be within the MX2 syllabus, but if you differentiate the expression
(1+b^2)} + \frac {a+b}{\sqrt{(1+a^2)(1+b^2)}} )
twice, as a function of and then as a function of
and then as a function of 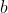 , it can be shown that there is exactly one point in the unit square
, it can be shown that there is exactly one point in the unit square 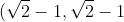) that is a stationary point in both cases.
that is a stationary point in both cases.
(The derivative actually only needs to be taken once, as and
and 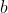 are symmetric in the expression.)
are symmetric in the expression.)
This point can be shown to be a local maximum by analysing the two derivatives.
The function attains the value of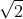 at this point, so
at this point, so 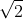 must be its maximum value over the unit square. (It's actually a global maximum, but that isn't necessary to show.)
must be its maximum value over the unit square. (It's actually a global maximum, but that isn't necessary to show.)
This may not quite be within the MX2 syllabus, but if you differentiate the expression
twice, as a function of
(The derivative actually only needs to be taken once, as
This point can be shown to be a local maximum by analysing the two derivatives.
The function attains the value of
One slight cheat would be to say that the equation that we have is symmetrical in  and
and  and thus that the max / min likely lies on the diagonal
and thus that the max / min likely lies on the diagonal 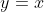 . We would then need to examine the function:
. We would then need to examine the function:
^2} + \frac{2x}{1+x^2})
in the domain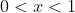 . We would then find:
. We would then find:
}{\left(x^2+1\right)^2})
which is zero when^2 = 2) and so the only stationary point in the domain corresponds to
and so the only stationary point in the domain corresponds to 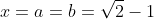 , as @fan96 stated.
, as @fan96 stated.
}{\left(x^2+1\right)^3} \\ \text{At $x = \sqrt{2} - 1$} \qquad \frac{d^2F}{dx^2} &= \frac{4\left[\left(\sqrt{2}\right)^3 -3\left(\sqrt{2}\right)^2 + 3\left(\sqrt{2}\right)^1 - 1 + 3\left(3 - 2\sqrt{2}\right) - 3\left(\sqrt{2} - 1\right) - 1\right]}{\left(3 - 2\sqrt{2} +1\right)^3} \\ &= \frac{4\left(2\sqrt{2} - 6 + 3\sqrt{2} - 1 + 9 - 6\sqrt{2} - 3\sqrt{2} + 3 - 1\right)}{\left(4 - 2\sqrt{2}\right)^3} \\ &= \frac{4\left(4 - 4\sqrt{2}\right)}{\left[2\left(2 - \sqrt{2}\right)\right]^3} \\ &= \frac{16\left(1 - \sqrt{2}\right)}{8\left[2^3 - 3(2)^2\sqrt{2} + 3(2)\left(\sqrt{2}\right)^2 - \left(\sqrt{2}\right)^3\right]} \\ &= \frac{2\left(1 - \sqrt{2}\right)}{8 - 12\sqrt{2} + 12 - 2\sqrt{2}} \\ &= \frac{2\left(1 - \sqrt{2}\right)}{2\left(10 - 7\sqrt{2}\right)} \times \frac{10+7\sqrt{2}}{10+7\sqrt{2}} \\ &= \frac{10+7\sqrt{2} - 10\sqrt{2}-7 \times 2}{10^2-\left(7\sqrt{2}\right)^2} \\ &= -\frac{4 + 3\sqrt{2}}{2} \end{align*})
Proving that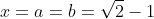 corresponds to a maximum.
corresponds to a maximum.
Substituting will show that
will show that 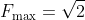 and thus completes the proof of the inequality.
and thus completes the proof of the inequality.
I don't plan to type it out, but I have checked, and when , we get
, we get
^2} = \frac{\sqrt{2}}{2})
and
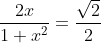
and thus get
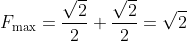
in the domain
which is zero when
Proving that
Substituting
I don't plan to type it out, but I have checked, and when
and
and thus get
Last edited:
that is some shoddy writing lol
Paradoxica
-insert title here-
Random observation I want to make. Let
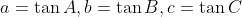
Then the problem reduces to maximising
 + \cos(2B) + 2\cos C )
subject to the constraint
 = 0)
and A,B,C are acute angles.
I don't know if this has a nice geometric interpretation, but if anyone has one, feel free to share it.
Edit: oh this was the solution described two posts above
Then the problem reduces to maximising
subject to the constraint
and A,B,C are acute angles.
I don't know if this has a nice geometric interpretation, but if anyone has one, feel free to share it.
Edit: oh this was the solution described two posts above
Last edited: