can you spot any errors in m working?
I'm not keen on some of the setting out, but the working looks ok to me.
I see where you are using less than / less than or equal to signs and note that they would disappear if you stated the strong induction more formally, such as:
Theorem: If
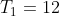
,
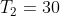
, and
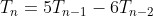
for all integers
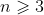
show that
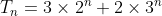
for all positive integers

.
Proof: By induction on
 A
A In order to use the identity in part
B, the general form must be shown to be true for the cases
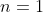
and
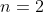
.
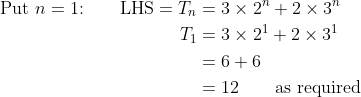
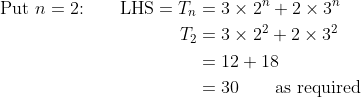
So, we know that the result is true for the cases
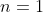
and
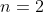
.
B Now, let
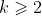
be a value of

such that the result is true for both
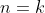 and
and 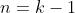
. That is,
}) and
and
})
We must now prove that the result is true for
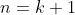
. That is, we must prove that

} \\ &= 5T_k - 6T_{k-1} \\ &= 5\left(3 \times 2^k + 2 \times 3^k\right) - 6\left(3 \times 2^{k-1} + 2 \times 3^{k-1}\right) \qquad \qquad \text{using the induction hypotheses (**) and (***)} \\ &= 15 \times 2^k + 10 \times 3^k - 2 \times 3 \times 3 \times 2^{k-1} - 2 \times 3 \times 2 \times 3^{k-1} \\ &= 15 \times 2^k + 10 \times 3^k - 9 \times 2^{k-1+1} - 4 \times 3^{k-1+1} \\ &= (15 - 9) \times 2^k + (10 - 4) \times 3^k \\ &= 2 \times 3 \times 2^k + 2 \times 3 \times 3^k \\ &= 3 \times 2^{k+1} + 2 \times 3^{k+1} \\ &= \text{ RHS} \end{align*})
So,
if the result is true for both
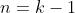 and
and 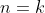
, then it must also be true for
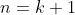
.
C It follows from
A and
B by the process of mathematical induction that the result must be true for all positive integers

.
----
If you use the stronger form of induction (making the assumption for all integers
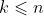
, the only change would be to the start of part
B, which would become:
B Now, let

be a value of

such that the result is true for all
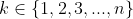
. In particular, this means that:
etc
Note that this stronger assumption still requires that the result be established in part A for
both 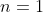 and
and 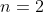
because invoking the recurrence relation requires knowledge of the truth of the general formula for the two preceding cases. Put another way, if you only proved the result for
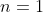
in part
A then it would not be proved for
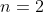
at any point - part
B works only if every case up to

is true and then uses the recurrence relation to establish the result for
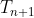
... but I can't say
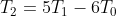
as there is no
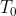
, and so part
B cannot prove
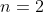
from
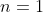
. Part
B proves the general formula for
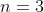
and every subsequent integer from knowing the formula is true for
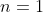
and
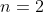
, but those initial cases must be established separately, which is the purpose of part
A, of course.
This is one reason that I prefer the weaker strong assumption in part
B that I gave above - assume for
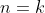
and
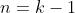
- because it is then obvious that my part
A needs to establish two initial values. Making the stronger assumption of truth for
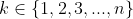
may only require establishing a single initial value in part
A, but it may (as in this case) require two initial values, and it is easy to not fully consider what is required in part
A for a valid and complete proof.
---
Does this clarify what you are asking?
, in order to use the relation in the second part of the proof, the preceding two values of
(that is,
and
) need to be known. You will thus need an assumption like
for both the cases n = 1 and n = 2.
.
instead of
, would we use n>=k instead of n=<k

instead of
, would we use n>=k instead of n=<k
