(a) If upwards is positive, then the acceleration due to gravity (10 m/s
2) is in the negative direction (ie. downwards). So, you have as your starting equation of motion
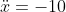
which, after integration, should give
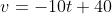
and
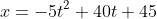
(c) is asking for the time at which
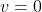
and the height (

) at that time.
(d) is asking you to show that the time (
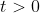
) at which
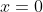
is
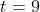
and (e) asks for

at that time.
(f) asks for

at
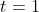
and
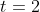
.
(g) asks for average velocity in the second second, which is the change in displacement (
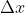
) divided by the change in time (
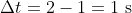
).