[Complex Numbers] Ex 1E Q22) | [Solved] (1 Viewer)
- Thread starter A1La5
- Start date
https://boredofstudies.org/threads/harder-complex-number-question.181881/Hello, I am stuck on this question.
View attachment 31910
I feel like I am on the right track with this, but I'm missing something small. My working out is as follows (sorry for it being all over the place..) - what have I missed?
Exact same question was answered here.
@A1La5, 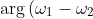}) is not the exterior angle of the triangle that you have drawn. Leaving aside that this argument is negative and the angle that you are calling the exterior angle is positive, the exterior angle of a triangle at a vertex must be between one of the sides that meet at that vertex and the other side the meets at that vertex produced.
is not the exterior angle of the triangle that you have drawn. Leaving aside that this argument is negative and the angle that you are calling the exterior angle is positive, the exterior angle of a triangle at a vertex must be between one of the sides that meet at that vertex and the other side the meets at that vertex produced.
The theorem you need is that co-interior angles on parallel lines are supplementary, with the angles being
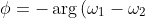}) (as
(as 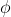 is a positive angle in a triangle but
is a positive angle in a triangle but 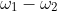 has a negative argument),
has a negative argument),
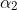 , and the third angle in the triangle that you have not named. Let's call it
, and the third angle in the triangle that you have not named. Let's call it 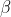 , so that your triangle has angles
, so that your triangle has angles 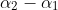 ,
, 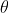 , and
, and 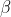 (though you don't actually need
(though you don't actually need 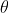 ).
).
You first need to find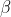 , so that a second application of co-interior angles with
, so that a second application of co-interior angles with 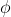 ,
, 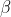 , and
, and 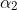 allows you to find
allows you to find 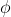 .
.
As you have recognised that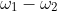 is a vector from
is a vector from 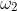 to
to 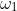 , you need only complete the parallelogram with
, you need only complete the parallelogram with 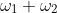 as the second diagonal (i.e., with vertices at
as the second diagonal (i.e., with vertices at 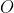 ,
, 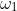 ,
, 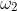 , and
, and 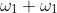 ).
).
Note that the interior angles of this parallelogram are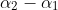 and
and 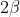 , and these angles are supplementary, which gives you that
, and these angles are supplementary, which gives you that
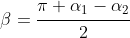
and from that you can find the size of
 - 2\alpha_2}{2} = \cfrac{\pi - \alpha_1 - \alpha_2}{2})
and hence you can determine the principal argument of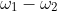 .
.
The theorem you need is that co-interior angles on parallel lines are supplementary, with the angles being
You first need to find
As you have recognised that
Note that the interior angles of this parallelogram are
and from that you can find the size of
and hence you can determine the principal argument of
It's worth noting that the thread that @Drdusk points to takes a different approach, finding my angle 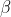 without completing the parallelogram by instead using the given fact that
without completing the parallelogram by instead using the given fact that  . This makes the triangle that @A1La5 drew above an isosceles triangle, from which it follows that
. This makes the triangle that @A1La5 drew above an isosceles triangle, from which it follows that 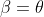 as these are its base angles. Both approaches are valid, of course.
as these are its base angles. Both approaches are valid, of course.
Damm, looks like I was a lot further from the solution then I thought. Thanks so much for your help!@A1La5,is not the exterior angle of the triangle that you have drawn. Leaving aside that this argument is negative and the angle that you are calling the exterior angle is positive, the exterior angle of a triangle at a vertex must be between one of the sides that meet at that vertex and the other side the meets at that vertex produced.
The theorem you need is that co-interior angles on parallel lines are supplementary, with the angles being
(as
is a positive angle in a triangle but
has a negative argument),
, and the third angle in the triangle that you have not named. Let's call it
, so that your triangle has angles
,
, and
(though you don't actually need
).
You first need to find, so that a second application of co-interior angles with
,
, and
allows you to find
.
As you have recognised thatis a vector from
to
, you need only complete the parallelogram with
as the second diagonal (i.e., with vertices at
,
,
, and
).
Note that the interior angles of this parallelogram areand
, and these angles are supplementary, which gives you that
and from that you can find the size of
and hence you can determine the principal argument of.
EDIT: @CM_Tutor, would the horizontal line drawn from
Last edited:
Yes, absolutely. It is the fact that it is parallel to theEDIT: @CM_Tutor, would the horizontal line drawn fromin the diagram be parallel to the positive real axis?
from which you can find
I am not seeing what pair of parallel lines you mean. In your second diagram, it looks like the angle you have labelled asIf so, then can we also use alternate angles + the angle sum of a triangle (with angles,
, and
) to calculate the value of
?
However, if you were to produce the side of the triangle that is represented by
This would be an alternative way to establish that
Yeah, guess I should've clarified. The two parallel lines that I'm talking about would be the horizontal line drawn fromI am not seeing what pair of parallel lines you mean.
In this diagram I have marked the two parallel sides I am referring to.
First, I used the fact that the triangle in the original diagram is isosceles (as both
Now, I redrew a triangle from this above diagram below.
The side opposite
After this the result just falls out, using your definition of
Last edited:




