When you take derivatives, think it as the rate of change of the function. So if you're trying to find a maxima/minima of the rate of change, you would need to find the rate of change of the rate of change; if that makes sense?, and then you would apply the same methods as you would normally by making the second derivative = 0. That's how I thought of it so it became less confusing, alternatively you can play around with desmos - I think getting a graphical intuition of these topics is WAY superior than an algebraic understanding, being able to visualise maths makes it way more easier and intuitive imo.
This sounds really stupid but try using desmos at times if you're struggling with exponential growth/decay, it makes way more sense after you understand the graph and you'll start to solve these questions through imagining the graph subconsciously as opposed to relying on algebra.

This is pretty cool on desmos as you can see the function is a logistics curve. The greatest rate of change always occurs at stat-points however this graph is always increasing however the rate at which it increases fluctuates. (The Green equation is the 2nd derivative), from this you can see that the Point of Inflection is the greatest rate of change and it explains why you would take the second derivative to be 0 since that is when this inflection occurs (draw a straight line down from the POI.
This isn't targeted at anyone specifically, I just want to give advice for anyone who comes across this thread and is struggling with some parts. I do think through playing around on desmos the topic will be more intuitive and fun as well as easier.
The answer is S=1000.
Lets call
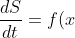)
Then,
= \frac{2S}{5} - \frac{S^2}{5000})
)}{dS}=\frac{2}{5}-\frac{2S}{5000})
Let
)}{dS} = 0)
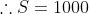
is a stat point
)^2}{d^2S}=\frac{-2}{5000} <0 )
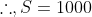
is a maximum in rate of change.
Ik this is a really pseudo and shady method but the other way is to think of it graphically because you should be accustomed to what type of graph that looks like.
I'm pretty sure that's the standard way of finding the answer but you chose to denote dy/dx as f(x) so I wouldn't say its shady; I think it makes more intuitive when you take the derivative to be f(x) as you show that the same method would be applied to find the maxima/minima of the second derivative.



is a stat point
is a maximum in rate of change.
