saltshaker
Member
- Joined
- Feb 13, 2021
- Messages
- 94
- Gender
- Male
- HSC
- 2023
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Yes becauseWhen I sub in x = -2 on the original eqn m gets deleted?
wait how did you find the equation of lYes becauseis a root of the equation.
Remember that the roots are, so you know that the sum of the roots is
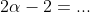
You use the point gradient formulawait how did you find the equation of l
You get the value of m by subbing the equation ofohh okay, how would you find m
Sorry would you be able to type the working out please?You get the value of m by subbing the equation ofinto
, then using the products and sum of roots to find the value of m.
