Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Qs (1 Viewer)
- Thread starter =)(=
- Start date
ExtremelyBoredUser
Bored Uni Student
For the first question, straight off the bat I would say (D). The rest of the choices seem wrong. Just square the equations and simultaneously solve them. A,B are dead giveaways that they're not a circle so its really between C and D and obviously C would produce extra remainder so its D.
wouldn't c be right because you can make cos t and sin t the subject and then use the Pythagorean idenitityFor the first question, straight off the bat I would say (D). The rest of the choices seem wrong. Just square the equations and simultaneously solve them. A,B are dead giveaways that they're not a circle so its really between C and D and obviously C would produce extra remainder so its D.
ExtremelyBoredUser
Bored Uni Student
No because when you square the x and y terms.wouldn't c be right because you can make cos t and sin t the subject and then use the Pythagorean idenitity
Hence you can't apply Pythagorean identity to simplify it to get a number value. The dead giveaway for this is that there's a 2 in front of cost so there's no way it would be able to get a clean factorisation which would eliminate the cos and sins.
For (D) you would get
Hence the eqn would be
Last edited:
Life'sHard
Well-Known Member
- Joined
- May 24, 2021
- Messages
- 1,101
- Gender
- Male
- HSC
- 2021
- Uni Grad
- 2025
Might as well start learning latex my guy. You're already typing it in latex format hahaha.No because when you square the x and y terms.
x^2 = 4cos^2t
y^2 = sin^2t
--------------
x^2 + y^2 = 4cos^2t + sin^2t
x^2 + y^2 = 4(cos^2t + 1/4sin^2t)
Hence you can't apply Pythagorean identity to simplify it to get a number value. The dead giveaway for this is that there's a 2 in front of cost so there's no way it would be able to get a clean factorisation which would eliminate the cos and sins.
For (D) you would get 8cos^2t + 8sin^2t if you simplify and factorising it 8(sin^2t+cos^2t) = 8(1).
Hence the eqn would be x^2 + y^2 = 8 so it would be the correct answer.
ExtremelyBoredUser
Bored Uni Student
The latex format doesn't show up on my screen? I know how to use it but it doesn't appear on my screen at all so I presume its the same for everyone?Might as well start learning latex my guy. You're already typing it in latex format hahaha.
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 561
- Gender
- Male
- HSC
- 2018
For part ii the general strategy is this given ^{2}, x > 1,) we see there we are required to find where the points of the inverse are the same as the given graph. Now we will apply the mirror
we see there we are required to find where the points of the inverse are the same as the given graph. Now we will apply the mirror 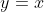 to make x the main ingredient. In this case what we will have is
to make x the main ingredient. In this case what we will have is 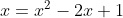 becoming
becoming 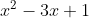 . There use the quadratic formula and we should obtain two solutions. The rest should be trivial because you just have to rely on what the question specified and one of the solutions will be within the domain and the other will not.
. There use the quadratic formula and we should obtain two solutions. The rest should be trivial because you just have to rely on what the question specified and one of the solutions will be within the domain and the other will not.
In general when they ask "find any value for x where=f^{-1}(x)) ," for me the general strategy will be to turn y into x because we are focusing on x and also for inverses the line
," for me the general strategy will be to turn y into x because we are focusing on x and also for inverses the line 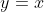 is used as a mirror to sketch the inverted graph. At this moment using the quadratic equation find the values of x and then if they give you the domain from the question apply the domain and you will be done. However, if you are required to sketch the inverse, different story. Now you have to swap x & y from the original function and make y the subject and why I say swap x & y is because the inverse is reflected in the line
is used as a mirror to sketch the inverted graph. At this moment using the quadratic equation find the values of x and then if they give you the domain from the question apply the domain and you will be done. However, if you are required to sketch the inverse, different story. Now you have to swap x & y from the original function and make y the subject and why I say swap x & y is because the inverse is reflected in the line 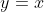 . Is there someone who can clarify what I said or make any corrections?
. Is there someone who can clarify what I said or make any corrections?
In general when they ask "find any value for x where
Last edited:
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 561
- Gender
- Male
- HSC
- 2018
There is the f(x) button and press that this is what you will obtainThe latex format doesn't show up on my screen? I know how to use it but it doesn't appear on my screen at all so I presume its the same for everyone?
I agree with @5uckerberg on solving =f^{-1}(x)) by noting that the intersections must occur on
by noting that the intersections must occur on 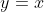 , and thus by solving
, and thus by solving  = x) .
.
A useful prior step can be to quickly sketch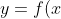 = (x-1)^2) and
and 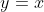 . Since
. Since 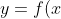) is a concave up parabola with vertex at
is a concave up parabola with vertex at ) and
and  -intercept at
-intercept at 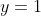 , sketching on
, sketching on 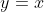 will immediately show that there should be two points of intersection to find, one somewhere in the domain
will immediately show that there should be two points of intersection to find, one somewhere in the domain 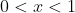 , and the other in
, and the other in 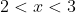 . This allows a quick quick on whether the results you find are reasonable.
. This allows a quick quick on whether the results you find are reasonable.
A useful prior step can be to quickly sketch
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 561
- Gender
- Male
- HSC
- 2018
To be fair one can do Q9 in a different way. I can say with parametric equations for a circle usually it can be written like this 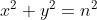 . All you gotta do is square both terms and see if they give something like this
. All you gotta do is square both terms and see if they give something like this 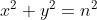 , if not then it is not a circle.
, if not then it is not a circle.
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 561
- Gender
- Male
- HSC
- 2018
Thank you CM tutor for debunking my idea, even though it works for one case.PS... That (D) in the MCQ is a circle can also be found by examining
but this wouldn't work as well as the method I posted above if the circle had a centre anywhere but the origin.
I would now bring up a schema for locus,
For circles
For ellipses
For hyperbolas
For lines
For the well-known asymptote
These are what you want to get at the end.
Last edited:
@5uckerberg, parametrised equations of lines aren't restricted to going through the origin. Option (B), above, has parametric equations 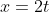 and
and 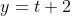 , which are the equivalent of the Cartesian equation is
, which are the equivalent of the Cartesian equation is 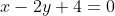 ... this doesn't fit the
... this doesn't fit the 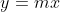 model that you have stated, so you might want to edit your post to expand the forms to
model that you have stated, so you might want to edit your post to expand the forms to 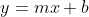 where
where 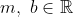 ... and FYI, the code I have used here is "m,\ b \in \mathbb{R}", rather than using \epsilon as you have.
... and FYI, the code I have used here is "m,\ b \in \mathbb{R}", rather than using \epsilon as you have.
Also, I think picking out the forms of ellipses and hyperbolae is likely beyond most MX1 expectations.
Finally, if you had something like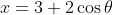 and
and 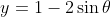 , the technique that is easiest is to recognise that:
, the technique that is easiest is to recognise that:

and thus use the Pythagorean identity:
^2 + \left(\cfrac{1-y}{2}\right)^2 &= 1 \\ (x-3)^2 + (1 - y)^2 &= 4 \\ (x-3)^2 + (y - 1)^2 &= 4 \qquad \qquad \text{as $(1 - y)^2 = 1 - 2y + y^2 = (y - 1)^2$} \end{align*})
to recognise the parametric equations describe a circle with centre at (3, 1) and radius = 2.
Also, I think picking out the forms of ellipses and hyperbolae is likely beyond most MX1 expectations.
Finally, if you had something like
and thus use the Pythagorean identity:
to recognise the parametric equations describe a circle with centre at (3, 1) and radius = 2.



