Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Help pls (1 Viewer)
- Thread starter =)(=
- Start date
For this you sub it x=-1 into P(x) knowing the remainder is 4. You do likewise for x=1 where P(x) is now -2. You now have two simultaneous equations that are easy to solve in order to find 'a' and 'b'. That's essentially what the question is asking.
GoldenMelon
Active Member
- Joined
- Oct 18, 2021
- Messages
- 105
- Gender
- Male
- HSC
- 2020
I think this one is D, but I’m not too sure. What I did was 10C6 which is the total amount of ways to select 6 from 10 students with no restrictions and then subtract 8C4 from that which is the amount of ways you can select the teams but including those two particular students.and also this pls
View attachment 32867
For this you do Total - complementary (bad case which is choosing those two particular students). Therefore the answer is 10C6 - 8C4 (since you have already chosen those two individuals).and also this pls
View attachment 32867
i got a=-3 and b=1 but what do i do from thereFor this you sub it x=-1 into P(x) knowing the remainder is 4. You do likewise for x=1 where P(x) is now -2. You now have two simultaneous equations that are easy to solve in order to find 'a' and 'b'. That's essentially what the question is asking.
ohh okay i thought you were allowed to have only one on the team since it said bothFor this you do Total - complementary (bad case which is choosing those two particular students). Therefore the answer is 10C6 - 8C4 (since you have already chosen those two individuals).
i did long division and got -2x +4you can do long division to find the remainder
Lol never ever do long division for these questions. They are meant to be solved using remainder theorem. Since you have found that a=-3 and b=1 then the answer is D since dividing P(x) by (x^2-1) is the same is dividing by (x+1)(x-1) which you can see are the ones in the question. Meaning P(x) = (x+1)(x-1)Q(x) +ax+b where a = -3 and b=1 (if you're correct)
ohhh okay so the (x+1)(x-1)Q(x) becomes 0 and your left with -3x +1 ?Lol never ever do long division for these questions. They are meant to be solved using remainder theorem. Since you have found that a=-3 and b=1 then the answer is D since dividing P(x) by (x^2-1) is the same is dividing by (x+1)(x-1) which you can see are the ones in the question. Meaning P(x) = (x+1)(x-1)Q(x) +ax+b where a = -3 and b=1 (if you're correct)
@=)(=, the division algorithm says that when I divide a polynomial ) by a divisor,
by a divisor, ) , I get a quotient,
, I get a quotient, 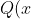) , and a remainder, related by:
, and a remainder, related by:
 = d(x)Q(x) + R(x))
The polynomial is divisible by) if and only if
if and only if  = 0) .
.
In this question, we need) in the form
in the form  = d(x)Q(x) + R(x)) where
where  = x^2 - 1) .
.
You can approach this by starting to look for the values and
and  given in the formula
given in the formula  = x^3 + 3x^2 + ax + b) , but you actually don't need to find
, but you actually don't need to find  and
and  unless they help you to get the polynomial in the appropriate form for the division algorithm. What you actually need to do is consider your
unless they help you to get the polynomial in the appropriate form for the division algorithm. What you actually need to do is consider your ) and how to get the required form.
and how to get the required form.
Now, since) is of degree 2,
is of degree 2, ) can be of degree no more than 1, so let
can be of degree no more than 1, so let  = Ax + B) , so you have
, so you have
 = Q(x)\left(x^2 - 1\right) + Ax + B)
Note that these constants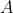 and
and 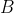 are not the same as
are not the same as  and
and  , so perhaps different symbols might be wise.
, so perhaps different symbols might be wise.
In any case, we are given that the remainder is -4 on division by) , so
, so  = 4) by the remainder theorem:
by the remainder theorem:
 &= 4 \\ Q(-1)\left[(-1)^2 - 1\right] + A(-1) + B &= 4 \\ Q(-1) \times 0 - A + B &= 4 \\ B - A &= 4 \end{align*})
Also, on division by) , the remainder is -2, so
, the remainder is -2, so  = -2) by the remainder theorem.
by the remainder theorem.
 &= -2 \\ Q(1)\left[(1)^2 - 1\right] + A(1) + B &= -2 \\ Q(1) \times 0 + A + B &= -2 \\ A + B &= -2 \end{align*})
Solving simultaneously, we get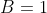 and
and 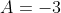 , and so
, and so  = \left(x^2 - 1\right)Q(x) - 3x + 1) and so the remainder on division by
and so the remainder on division by ) is
is  and the answer is D.
and the answer is D.
The polynomial is divisible by
In this question, we need
You can approach this by starting to look for the values
Now, since
Note that these constants
In any case, we are given that the remainder is -4 on division by
Also, on division by
Solving simultaneously, we get
Just like if I divide 73 by 10, I get 7 with a remainder of 3, that isohhh okay so the (x+1)(x-1)Q(x) becomes 0 and your left with -3x +1 ?
Starting number = divisor x quotient + remainder


