Okay, this question. Hmm sounds familiar if the union of a and b is

then the intersection of the complement of A and B is just the cresent in B which can be found from the fact that the intersection of A and B is just
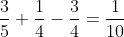
and then to find the intersection of the complement of A and B we do

Part b is like this If A and B are mutually exclusive what happens is that suppose A and B are separate circles that do not touch what we have here is the complement of A is everything outside of A and the intersection of the complement of A and B is just B giving us
