From the letters of the word SHOWDOWN, four-letter words were formed. How many words began and ended with a vowel? (1 Viewer)

[tk8]

The answer is apparently 121, but I got 21…
thanks!

 

[LennonTheLemon]

If it must end and begin with a vowel the two O's must be fixed on each side of the four-letter word:
O __ __ O
Of the remaining letters S, H, W, W, D, N, there's case 1 where you get OWWO and since it is a palindrome it can only be done one way. Then there's case 2, picking one W and any other remaining letter in the middle. Finally, there is case 3 where you pick any remaining letters except for the W's in the middle. So 1 + 5P2 + 4P2 = 33. Maybe there is more cases but I'm not sure. 121 is a very large SUS number.

 

[5uckerberg]

An interesting take on this question would be to take the two Os as one possibility.
Next because you have 6 letters and we treat the Ws as one then we have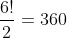 because you have to take into account the Ws in the list of letters.
Thirdly because you are going to have 3 situations you will have to do 360 divided by 3 which gives us 120 and lastly 1 + 120 = 121 ways.
If someone can come with a better explanation write it down.

 

[dan964]

4 letter words:
Case 1: both W - OWWO - 1
Case 2: one W - OW?O or O?WO - 8
Case 3: no W - O??O - 12 (4*3, since non replacement)

So answer is 21, your textbook is wrong unless it counts duplicates.

 

[tk8]

4 letter words:
Case 1: both W - OWWO - 1
Case 2: one W - OW?O or O?WO - 8
Case 3: no W - O??O - 12 (4*3, since non replacement)

So answer is 21, your textbook is wrong unless it counts duplicates.

That's what I did! Glad to know that I at least ended up with the correct answer

 

[5uckerberg]

4 letter words:
Case 1: both W - OWWO - 1
Case 2: one W - OW?O or O?WO - 8
Case 3: no W - O??O - 12 (4*3, since non replacement)

So answer is 21, your textbook is wrong unless it counts duplicates.

I just take it that it counts duplicates because there is no place in the question that says without repetition or replacement for collecting things from a box.

 

[dan964]

I just take it that it counts duplicates because there is no place in the question that says without repetition or replacement for collecting things from a box.

nope that is not right, if it counts duplicates, then it would be 60
Case 1: 4
Case 2: 8*4 = 32
Case 3: 2*4*3 = 24

With replacement then it would be just 2*8*8*2 which is clearly even.

 

[5uckerberg]

nope that is not right, if it counts duplicates, then it would be 60
Case 1: 4
Case 2: 8*4 = 32
Case 3: 2*4*3 = 24

With replacement then it would be just 2*8*8*2 which is clearly even.

I see it there. No worries I reckon the way I did the solution was the way the textbook wrote the solution but I can say now that 21 is the right answer because of the fact that we are assuming this is a non-replacement type of question.

 

[dan964]

An interesting take on this question would be to take the two Os as one possibility.
Next because you have 6 letters and we treat the Ws as one then we have because you have to take into account the Ws in the list of letters.
Thirdly because you are going to have 3 situations you will have to do 360 divided by 3 which gives us 120 and lastly 1 + 120 = 121 ways.
If someone can come with a better explanation write it down.

6!/2 (6P4) is invalid because you forgot that if you pick O or W the first time you have to put it back in but only those letters and only the first time (so you cannot have OWWW ). Basically if I’m pulling the letters out of a hat I’m twice as likely to pull out an O or W then any other letter. (Your method does assume non replacement)

Dividing by 3 is also incorrect/invalid because the 3 “situations” (i assume from context what these are) are not equally likely. Not that it was clear what the situations are anyways. By your logic, you would actually be dividing a different number by 6 (or maybe 36 if doing replacement) not 3 (since we only consider cases where the first letter has to be an O).
Thirdly where does the +1 come from? That was not even justified.

Your method actually (ignoring duplicates) gives you double the answer of the number of 4 letter words that start with O and only use each letter uniquely once. (i.e no words with two O or two W)

 

[dan964]

I see it there. No worries I reckon the way I did the solution was the way the textbook wrote the solution but I can say now that 21 is the right answer because of the fact that we are assuming this is a non-replacement type of question.

See response above. Cannot work out how to multi-quote on the phone

 

[5uckerberg]

6!/2 (6P4) is invalid because you forgot that if you pick O or W the first time you have to put it back in but only those letters and only the first time (so you cannot have OWWW ). Basically if I’m pulling the letters out of a hat I’m twice as likely to pull out an O or W then any other letter. (Your method does assume non replacement)

Dividing by 3 is also incorrect/invalid because the 3 “situations” (i assume from context what these are) are not equally likely. Not that it was clear what the situations are anyways. By your logic, you would actually be dividing a different number by 6 (or maybe 36 if doing replacement) not 3 (since we only consider cases where the first letter has to be an O).
Thirdly where does the +1 come from? That was not even justified.

Your method actually (ignoring duplicates) gives you double the answer of the number of 4 letter words that start with O and only use each letter uniquely once. (i.e no words with two O or two W)

Oh right, so you found the textbook's mistake congrats on saving tk8 the confusion of debating which answer is right. Thank you for clarifying the issue here.

 

[dan964]

Oh right, so you found the textbook's mistake congrats on saving tk8 the confusion of debating which answer is right. Thank you for clarifying the issue here.

The textbooks mistake was probably a misprint or typo , I doubt they used your method haha