-
Best of luck to the class of 2025 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Maximisation and Minimisation in Geometry Question (1 Viewer)
- Thread starter tk8
- Start date
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 560
- Gender
- Male
- HSC
- 2018
@tk8 Here is the solution. I want you to check your work to see where you tripped yourself in the path of solving these two parts.
Part c
To start off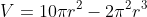
Then,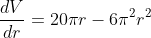
Note this means the rate of volume divided by the rate of radius.
So if we want to find the maximum or minimum then the rate has to be resting or in this case 0.
Using this knowledge we have determined that
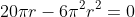
Factorising we can automatically see that
=0)
Note here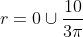 .
.
To confirm do the second derivative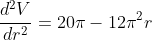
Did thee question say there was a minimum volume? Well, nope it said the maximum volume.
So instead sub in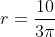 and you should get
and you should get 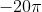 which is considerably smaller than 0 so thus, you have confirmed that there is a maximum.
which is considerably smaller than 0 so thus, you have confirmed that there is a maximum.
Can you spot where you went wrong in your working
Part d
Since we have proven that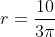 then put
then put 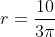 into
into )
Watch as the magic unfolds
)
)
This simply becomes
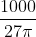
and you can do the rest
There must have been an error carried forward. Find it.
Part c
To start off
Then,
Note this means the rate of volume divided by the rate of radius.
So if we want to find the maximum or minimum then the rate has to be resting or in this case 0.
Using this knowledge we have determined that
Factorising we can automatically see that
Note here
To confirm do the second derivative
Did thee question say there was a minimum volume? Well, nope it said the maximum volume.
So instead sub in
Can you spot where you went wrong in your working
Part d
Since we have proven that
Watch as the magic unfolds
This simply becomes
and you can do the rest
There must have been an error carried forward. Find it.
Last edited:
have a look at my solutions attached
Attachments
-
364.8 KB Views: 10
tk8
Member
- Joined
- Nov 16, 2021
- Messages
- 63
- Gender
- Undisclosed
- HSC
- 2024
Thanks so much!have a look at my solutions attached
tk8
Member
- Joined
- Nov 16, 2021
- Messages
- 63
- Gender
- Undisclosed
- HSC
- 2024
I appreciate the detail, thanks!@tk8 Here is the solution. I want you to check your work to see where you tripped yourself in the path of solving these two parts.
Part c
To start off
Then,
Note this means the rate of volume divided by the rate of radius.
So if we want to find the maximum or minimum then the rate has to be resting or in this case 0.
Using this knowledge we have determined that
Factorising we can automatically see that
Note here.
To confirm do the second derivative
Did thee question say there was a minimum volume? Well, nope it said the maximum volume.
So instead sub inand you should get
which is considerably smaller than 0 so thus, you have confirmed that there is a maximum.
Can you spot where you went wrong in your working
Part d
Since we have proven thatthen put
into
Watch as the magic unfolds
This simply becomes
and you can do the rest
There must have been an error carried forward. Find it.
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 560
- Gender
- Male
- HSC
- 2018
To start off we need to know the rate of change in volume per the rate of change in height which is written asCould you guys also please help me with part c) and part d) of the attached question?
I don't know how to prove the maximisation for part c), and I am not attaining the correct ratio for part d).
Thanks
View attachment 35017
Once the foundation is set we want to find the maximum or minimum and we need to show that by stating the rate of change is zero as you know the rate of change interrupts us from finding the maximum or the minimum.
In this case let
In fact
There,
Finsihing it off
Somebody wanted to rationalise the cylinder.
part d)
Sub in
There we will have
At this point we will have
Simplifying further it becomes
At this point compare with the volume of the sphere so now we have
Volume of sphere : Volume of cylinder
At this point you can say the ratio of the volume of sphere to the maximum value of the cylinder is
Have a good lunch break @tk8
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 560
- Gender
- Male
- HSC
- 2018
To prove part c for the maximum do the second derivative. Note that if the result is negative then you have proven that it’s the maximum.



