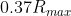although, i think if f(x) is strictly increasing then (A) is correct.Ah shit yea that makes sense
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Mathematics Extension 1 HSC thoughts (1 Viewer)
- Thread starter jdad1
- Start date
- Joined
- Feb 16, 2005
- Messages
- 8,577
- Gender
- Male
- HSC
- 2006
Scaling is applied on raw marks. See below for a high level summary of the process:I think UAC uses only the HSC aligned mark and then scales that based on their own thing, which is skewed non-linearly from the very high marks (which is what adjusts it so that a student who gets 98-->100 is rewarded over the 67-->90), which is what counts to your aggregrate:
I'm not sure nesa even gives UAC the raw marks? Not sure of this though, don't quote me on that
View attachment 36772
Flowchart of how HSC marks and ATAR are determined
Hi all, We have received a lot of questions on the aspects of the HSC and ATAR calculation process ranging from scaling, moderating and aligning. It has become apparent that some confusion exists on how the process works overall. This is important to understand before diving into the finer...
ExtremelyBoredUser
Bored Uni Student
Nah nah pre sure D is right because it doesnt specify italthough, i think if f(x) is strictly increasing then (A) is correct.
yeah D is right, but if it did it would be A hahaNah nah pre sure D is right because it doesnt specify it
Run hard@thehsc
Well-Known Member
- Joined
- Oct 7, 2021
- Messages
- 784
- Gender
- Male
- HSC
- 2022
Wait so scaling obs applies on the corresponding raw of your average HSC mark right?
thanks, that's very helpful!Scaling is applied on raw marks. See below for a high level summary of the process:
Flowchart of how HSC marks and ATAR are determined
Hi all, We have received a lot of questions on the aspects of the HSC and ATAR calculation process ranging from scaling, moderating and aligning. It has become apparent that some confusion exists on how the process works overall. This is important to understand before diving into the finer...boredofstudies.org
yanujw
Well-Known Member
- Joined
- May 23, 2020
- Messages
- 338
- Gender
- Male
- HSC
- 2022
Just another change to bring to your attention is that 6 is (C) because the projection onto that vector must have equal i and j components.oh you know what. D is correct
consider f(x) = 1/x
f-1(x) is 1/x
they intersect everywhere, not only on y=x
answer is D
thanks for that ill change it and upload new ones later
Last edited:
Two thoughts on notme's answers;

(btw, thanks notme for the very fast answers )
)
- I'm pretty sure that 13c is false. It says is g the inverse of f, NOT the inverse function of f. Isn't the inverse simply the reflection in y=x? This would mean that arcsin(x) is not the inverse as it doesn't cover the full range of the inverse.
- For 14d, isn't the number of no shows dependent on the number of tickets that are sold? n isn't 350 (the number of seats), it's the number of tickets sold, as each ticketholder can be considered a bernoulli trial of whether they will show up or not. (Is how I read the question)
(btw, thanks notme for the very fast answers
Last edited:
Daedalus13
New Member
- Joined
- Oct 14, 2022
- Messages
- 16
- Gender
- Male
- HSC
- 2022
If you consider f(x)= x^3 and its inverse, the intersection at the origin has the tangents to the graph be perpendicular. So D is also incorrect?Nah nah pre sure D is right because it doesnt specify it
Edit: I realised that a vertical tangent means it f'(x) is not defined for the inverse for all real x.
Last edited:
inverse of x^3 does not have a defined derivative at x = 0If you consider f(x)= x^3 and its inverse, the intersection at the origin has the tangents to the graph be perpendicular. So D is also incorrect?
how would you reason it isn't B by that judgement? mid-exam i intuitively ruled off C because the vector u was in the opposite direction, thus there could be no component acting in the same way (which is what projection vectors are)Just another change to bring to your attention is that 6 is (C) because the projection onto that vector must have equal i and j components.
Also, 8 is (A) by considering an isosceles triangle with unit length and requiring the joining side to have length to be less than 1, which can occur up to the point that the triangle is equilateral, therefore less than pi/3 angle within the vectors.Nvm you were correct, welp just discovered another question I got wrong lol.
Daedalus13
New Member
- Joined
- Oct 14, 2022
- Messages
- 16
- Gender
- Male
- HSC
- 2022
Also the diagram was 'DRAWN TO SCALE', so 3.2 is much too large.how would you reason it isn't B by that judgement? mid-exam i intuitively ruled off C because the vector u was in the opposite direction, thus there could be no component acting in the same way (which is what projection vectors are)
mmmmmmmmaaaaaaa
Well-Known Member
- Joined
- Jun 11, 2021
- Messages
- 1,378
- Gender
- Undisclosed
- HSC
- N/A
HOw did people do 14b? the vector proof
Your comment on 13c, this was what I wrote as well. Something like g(x)=arcsinx is defined only for x [-1,1], but f(x)=sinx is defined for x across the reals. They even specified x across all real for f(x)=sinx, which to me made it seem clear they wanted you to conclude false due to domain/range non-equivalence.Two thoughts on notme's answers;
I could be completely wrong though
- I'm pretty sure that 13c is false. It says is g the inverse of f, NOT the inverse function of f. Isn't the inverse simply the reflection in y=x? This would mean that arcsin(x) is not the inverse as it doesn't cover the full range of the inverse.
- For 14d, isn't the number of no shows dependent on the number of tickets that are sold? n isn't 350 (the number of seats), it's the number of tickets sold, as each ticketholder can be considered a bernoulli trial of whether they will show up or not. (Is how I read the question)

you're right lol that completely escaped me.Just another change to bring to your attention is that 6 is (C) because the projection onto that vector must have equal i and j components.
I'm doing more correct ones now sorry for the inconvenience guys
do the regular projectile motion things to find time of flight (let y=0 etc), solve simultaneously for x and rearrange, you're left with:HOw did people do 14b? the vector proof
Then, optimise the function on the LHS and you get the maximum value of
Daedalus13
New Member
- Joined
- Oct 14, 2022
- Messages
- 16
- Gender
- Male
- HSC
- 2022
I believe 6 C is incorrect, it should be B (see above).you're right lol that completely escaped me.
I'm doing more correct ones now sorry for the inconvenience guys
Also the diagram was 'DRAWN TO SCALE', so 3.2 is much too large.
- Joined
- Feb 16, 2005
- Messages
- 8,577
- Gender
- Male
- HSC
- 2006
Correct. Your raw mark branches off into two different types of transformations:Wait so scaling obs applies on the corresponding raw of your average HSC mark right?
- Aligning (for your HSC certificate)
- Scaling (for your ATAR)
- Joined
- Feb 16, 2005
- Messages
- 8,577
- Gender
- Male
- HSC
- 2006
Yep. See Q14c) in this year’s BoS trials for Ext2although, i think if f(x) is strictly increasing then (A) is correct.
mmmmmmmmaaaaaaa
Well-Known Member
- Joined
- Jun 11, 2021
- Messages
- 1,378
- Gender
- Undisclosed
- HSC
- N/A
The one before that, the inequality onedo the regular projectile motion things to find time of flight (let y=0 etc), solve simultaneously for x and rearrange, you're left with:
Then, optimise the function on the LHS and you get the maximum value ofis equal to 0.369..., so then all other d must be below