Help with differentiation question (1 Viewer)

[Scimat]

Hey guys can anyone provide the solution for part b of this question.

 

[jimmysmith560]

The below working included in a post from an older thread appears to reach one of the two equations, being 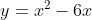. Perhaps you could use this to assist you in finding the other equation?

b) Hence find the equations of any quadratics that pass through the origin and are tangent to both y= -2x - 4 and to y = 8x -49

I've never tried one like this but I'll give it a shot.

If the quadratic passes through the origin then y = ax² +bx + c, where c=0
y= -2x-4, gradient = -2 and y intercept = -4 (1)
y=8x -49, gradient = 8 and y intercept = -49 (2)

combining (1) with the expression obtained in 1.a) [y= c - (m-b)²/4a] but now where c=0
-4 = -(-2-b)²/4a ----> (b+2)²/4 = 4a (3)

combining (2) with the expression obtained in a)
-49 = -(8-b)²/4a ----> (8-b)²/49 = 4a (4)

Using (3) and (4)
(b+2)²/4 = (8-b)²/49
(b+2)/2 = (8-b)/7
(here I'm slightly unsure about where to take ± so I'll just take one. If someone could correct me on this and show me the convention that'd be cool.)

±7(b+2) = 16 - 2b
either b = 2/9 or b=-6

using (b+2)² = 4a
16 = 16a ---> a =1 when b=-6 -----> quadratic y = x² -6x

using b=2/9 seems to give something that isn't an answer. ^ There's one of them in any case.

I hope this helps!

 

[Scimat]

Thank you!

 

[hornsbystudylad]

Hey guys can anyone provide the solution for part b of this question.

View attachment 36997

^worked ans i found for your question
hope it helped