trig equation qn (1 Viewer)

Masaken · Jan 6, 2023

need help on what I may have done wrong with this qn? the answers say the solutions are only plus minus pi/2 + k2pi (which makes no sense to me because sin(-90) = -1? or are the answers just scuffed? thanks in advance

5uckerberg · Jan 6, 2023

Masaken said:
need help on what I may have done wrong with this qn? the answers say the solutions are only plus minus pi/2 + k2pi (which makes no sense to me because sin(-90) = -1? or are the answers just scuffed? thanks in advance

View attachment 37348

With the $\frac{-\pi}{2}+2k\pi$ solution I believe that they took the negative root as well which can be justified through similar working.

Masaken · Jan 6, 2023

5uckerberg said:
With the $\frac{-\pi}{2}+2k\pi$ solution I believe that they took the negative root as well which can be justified through similar working.

oh okay, what kind of working would you need to put in? also, the solutions only list plus minus pi/2 + k2pi, are the solutions for sinx = -1/2 correct as well? i have no idea why they wouldn't be correct (or why they would be solutions for -1/2 would be omitted in the first place, unless i've read or done the qn wrong?)

5uckerberg · Jan 6, 2023

I believe that instead of 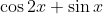$\cos{2x}+\sin{x}$ the question is 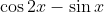$\cos{2x}-\sin{x}$ and next step you just have
$1-2\sin^{2}x-\sin{x}=0$
$2\sin^{2}x+\sin{x}-1=0$
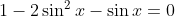
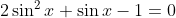
$\left(\sin{x}+1\right)\left(2\sin{x}-1\right)$
$\sin{x}=-1, \frac{1}{2}$
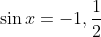
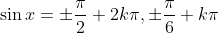$\sin{x}=\pm\frac{\pi}{2}+2k\pi, \pm\frac{\pi}{6}+k\pi$ . This I believe is the best I can come up with, I mean we can experiment with the values here.

Masaken · Jan 6, 2023

i mean it's strange that the sign in the question would have to be changed because i have no idea how you would incorporate that into the working out but i guess the question is probably scuffed itself :/ thanks for the help

Masaken · Jan 6, 2023

5uckerberg said:
I believe that instead of $\cos{2x}+\sin{x}$ the question is $\cos{2x}-\sin{x}$ and next step you just have
$1-2\sin^{2}x-\sin{x}=0$
$2\sin^{2}x+\sin{x}-1=0$
$\left(\sin{x}+1\right)\left(2\sin{x}-1\right)$
$\sin{x}=-1, \frac{1}{2}$
$\sin{x}=\pm\frac{\pi}{2}+2k\pi, \pm\frac{\pi}{6}+k\pi$ . This I believe is the best I can come up with, I mean we can experiment with the values here.

i re-did the question based off of this and ended up getting the appropriate solutions, it didn't seem obvious to me before, but rather than simplifying 1 + cot^2(x) to csc^2(x), i changed cot to cos/sin, then with some simplifying you end up with cos2x + |sinx| = 0, then you solve considering two separate cases where sinx > 0 (or equal to as well) or sinx < 0, then ended up getting the correct answers (just plus minus pi/2 + k2pi), thanks for the help

5uckerberg · Jan 6, 2023

Masaken said:
i re-did the question based off of this and ended up getting the appropriate solutions, it didn't seem obvious to me before, but rather than simplifying 1 + cot^2(x) to csc^2(x), i changed cot to cos/sin, then with some simplifying you end up with cos2x + |sinx| = 0, then you solve considering two separate cases where sinx > 0 (or equal to as well) or sinx < 0, then ended up getting the correct answers (just plus minus pi/2 + k2pi), thanks for the help

You can actually rule out the $\pm\frac{\pi}{6}+k\pi$ solution because the equation does not match.

Average Boreduser · Jan 6, 2023

Was it incorrect? I got same answers as you did

Masaken · Jan 6, 2023

Pethmin said:
Was it incorrect? I got same answers as you did

the answers were plus minus pi/2 + k2pi only, the 11pi and 7pi one from my first attempt were wrong

5uckerberg · Jan 6, 2023

The problem is that 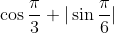$\cos{\frac{\pi}{3}}+|\sin\frac{\pi}{6}|$ is actually 1 which is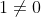 $1\neq{0}$

Average Boreduser · Jan 6, 2023

I got -pi/6+2npi, where n is an integer and pi/2+2npi, where n is an integer

Average Boreduser · Jan 6, 2023

Bro when tf did absolute values come in

Masaken · Jan 6, 2023

Pethmin said:
I got -pi/6+2npi, where n is an integer and pi/2+2npi, where n is an integer

could i see your working out?

5uckerberg · Jan 6, 2023

Pethmin said:
Was it incorrect? I got same answers as you did

i re-did the question based off of this and ended up getting the appropriate solutions, it didn't seem obvious to me before, but rather than simplifying 1 + cot^2(x) to csc^2(x), i changed cot to cos/sin, then with some simplifying you end up with cos2x + |sinx| = 0, then you solve considering two separate cases where sinx > 0 (or equal to as well) or sinx < 0, then ended up getting the correct answers (just plus minus pi/2 + k2pi), thanks for the help.

This is the key part.

5uckerberg · Jan 6, 2023

Pethmin said:
Bro when tf did absolute values come in

$\frac{1}{\sqrt{1+\cot^{2}x}}$ and that to help you understand here is a simple example $\sqrt{x^{2}}=\pm{x}=|x|$

Average Boreduser · Jan 6, 2023

Oh alr so we took +- from that so therefore lcscxl?
I'll see what I get w that

Masaken · Jan 6, 2023

Pethmin said:
Bro when tf did absolute values come in

sorry if the handwriting is completely illegible, lmk if you can't understand it

the key to getting the absolute value is what happens when you root sin^2(x), because you get both -sinx and sinx as solutions

Masaken · Jan 6, 2023

Masaken said:
sorry if the handwriting is completely illegible, lmk if you can't understand it
View attachment 37350
the key to getting the absolute value is what happens when you root sin^2(x), because you get both -sinx and sinx as solutions

or you can do |csc x| and get to |sinx|, oops

Average Boreduser · Jan 6, 2023

Yeah I got +- pi/2 +2npi, but theres also the other two solutions for pi/6+2npi tho...

Average Boreduser · Jan 6, 2023

do we disregard it as we would also need to pick up the (pi-(+-1/2)) which would lead to an additional 2 solutions?

trig equation qn (1 Viewer)

Unknown Member

Well-Known Member

Unknown Member

Well-Known Member

Unknown Member

Unknown Member

Well-Known Member

Rising Renewal

Unknown Member

Well-Known Member

Rising Renewal

Rising Renewal

Unknown Member

Well-Known Member

Well-Known Member

Rising Renewal

Unknown Member

Unknown Member

Rising Renewal

Rising Renewal

Users Who Are Viewing This Thread (Users: 0, Guests: 1)