I am sure that many people here have attempted the North Sydney Boys Extension 1 Trial from this year. I was looking at it earlier today and noticed that none of options provided are correct. I am wondering if anyone else has noticed that this MCQ does not offer a correct answer.
The question is:
The answer given is (B) but the correct answer is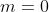
.
The approach taken is to look at the dot product. It is true that:
However, it is not true that:
because being perpendicular is not the only situation that leads to a dot product being zero... it also happens when one (or both) of the vectors is the zero vector. In other words, the first if-then statement above is correct (because vectors can only be perpendicular if they are non-zero), but the second if-then statement is drawing a conclusion from a zero dot product that only follows if the vectors are non-zero. The actual situation is that:
The calculation given in the solutions does lead to the conclusion that the answer is (B) as the dot product is zero if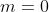 or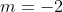 
.
The vector a - b = -(m + 2)i is parallel to the x-axis (if non-zero), and so can only be perpendicular to a vector parallel to the y-axis. This is the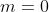 case, where a - b = -2i and b = mi - j = -j, which are indeed perpendicular.
When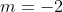, b = -2i - j which cannot be perpendicular to any vector ki, but can give a dot product of zero if k = 0. In this case,
we have a - b = -(-2 + 2)i = 0, which explains the result arising from looking at solutions of (a - b) . b = 0.
Has the mistake in this question been raised anywhere else or by anyone else, that I haven't seen?
The question is:
The answer given is (B) but the correct answer is
The approach taken is to look at the dot product. It is true that:
If two vectors u and v are perpendicular, then u . v = 0.
However, it is not true that:
If u . v = 0, then the two vectors u and v are perpendicular.
because being perpendicular is not the only situation that leads to a dot product being zero... it also happens when one (or both) of the vectors is the zero vector. In other words, the first if-then statement above is correct (because vectors can only be perpendicular if they are non-zero), but the second if-then statement is drawing a conclusion from a zero dot product that only follows if the vectors are non-zero. The actual situation is that:
Two vectors u and v have a dor product of zero (i.e. u . v = 0), if, and only if, the vectors are perpendicular or one or both of them is the zero vector.
The calculation given in the solutions does lead to the conclusion that the answer is (B) as the dot product is zero if
The vector a - b = -(m + 2)i is parallel to the x-axis (if non-zero), and so can only be perpendicular to a vector parallel to the y-axis. This is the
When
we have a - b = -(-2 + 2)i = 0, which explains the result arising from looking at solutions of (a - b) . b = 0.
Has the mistake in this question been raised anywhere else or by anyone else, that I haven't seen?
Last edited:
