Voolgdognng
New Member
- Joined
- Oct 24, 2023
- Messages
- 12
- Gender
- Male
- HSC
- 2023
How do i convert from parametric vector form to cartesian form for a plane
pre sure the conventional way isHow do i convert from parametric vector form to cartesian form for a plane
thanks, understood it nowpre sure the conventional way is
the eq of plane is given by
l = a + tu + mv where t,m are scalars and u,a,v are vectors
Find the normal of the plane by cross producting the direction vectors so n = u x v in this case
Apply the formula,
n * (x-a) = 0 (where n is the normal, x is (x,y,z) \in R3 and a is the vector and * means dot product)
and then expand and get your cartesian equation
cbf latexing sorry
for a draw the graoh, if your solution is bounded then thats it
for c) the harmonic series diverges so it is bounded above and the lower bound will just be 1
(a) is bounded above but not below as its a negative cubic, and so the region above
I think you can do polynomial long division for both and keep continuing the dividing process until you have a constant in the quotient, then whatever the quotient is is your answer. So for part 3 I think it would be 4*x-9 then for part 4 you could multiply the numerator by a constant to make the division process easier then you should end up with a linear expression as the quotient after dividing, then divide the quotient by the constant you multiplied the numerator by to get the final answer
for iii), i think if u do long division u can write the rational function as (4x-9) + 16/(x+1), and 16/(x+1) is O(x^-1) so the answer should just be 4x-9
dfn of O(f(x)): a function g(x) is O(f(x)) if there exists constants m and k such that for all x >=k, |g(x)|<= m|f(x)|thanks, but im confused with the 'Big O' and 'Little o' stuff
why would 16/(x+1) be O(1/x). and what does the 1/x even mean? would it be different if it was O(x)
lol i agree, thats what i did but it says im wrong???u can write det(WM^-1) as
u could also split the product up at the start to get
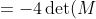)
detWM^-1Does anyone know what to do??
shouldnt it be k^8 det(A) as when a row/column is multiplied by a scalar k then det(A) increases by a factor of k? so since its an 8x8 matrix it would be k^8?keep in mind that det(kA) = k^2 det(A), you can check this for a 2x2 or 3x3 matrix if u like. i think that’s where the mistake is coming from
