asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,219
- Gender
- Undisclosed
- HSC
- 2012
8c) Last question
(c) The lengths of the sides of a triangle forman arithmetic progression and the largest angle of the triangle exceeds the smallest by 90◦. Find the ratio of the lengths of the sides.
What I've got so far:
a, b, c are in arithmetric series, so
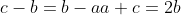
And if the largest angle exceeds the smallest by 90, then

Using sine rule

}}=\frac{c}{\sin\alpha}\\ b(\frac{2}{\sin\alpha}-\frac{1}{\cos{2\alpha}})=\frac{c}{\sin\alpha}\\ \frac{b}{c}=\frac{\cos{2\alpha}}{2\cos{2\alpha}-\sin\alpha})

Any help is appreciated. I don't know where I'm going with this lol. I generally hate geometry but this seemed like a fun problem.
(c) The lengths of the sides of a triangle forman arithmetic progression and the largest angle of the triangle exceeds the smallest by 90◦. Find the ratio of the lengths of the sides.
What I've got so far:

a, b, c are in arithmetric series, so
And if the largest angle exceeds the smallest by 90, then
Using sine rule
Any help is appreciated. I don't know where I'm going with this lol. I generally hate geometry but this seemed like a fun problem.
Last edited:
