2023 HSC Mathematics Extension 2 16c question mistake? (1 Viewer)

[sam davis hostage]

I've been looking at some solutions for this question, but they seem all incorrect. Videos include:

In the description of the video by Mind Your Decisions, there is a link to a tiktok by a James Ruse student who also provides a solution. I have a picture of their work attached below.

At some point, they all write something along the lines of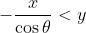 where . However, from this, they incorrectly conclude that , which comes from subbing in 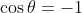. This is incorrect, because 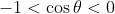. The correct conclusion should be that 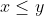, and the final region should have a solid line diagonal line below the origin. For example, if 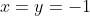, then 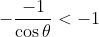will still be true, as . If you go to the desmos and add "/yf1efslc4b" after "calculator" in the url, you can see that the region should include y=x by dragging the z slider around.

I can't tell if this is a misunderstanding on my end or a collective error that everyone made. Any ideas?

 

[Sam14113]

Okay this is really interesting - I don't think you're correct but you've found something interesting and probably worth discussing.

The first thing to note is that the dotted line in the screenshot is labelled . That means that the point (-1, -1) isn't on the line at all, because exactly as you pointed out, .

But I think the interesting bit is I think you're interpreting the question as "Sketch the region where the inequality holds for all possible values of z, w which satisfy the restriction." However, everyone else seems to have interpreted the question as "Sketch the region where the inequality holds in terms of z, w." I think the way the question is worded, this is more appropriate, just because of the way that z and w seem to be referred to as constants rather than variables, but I'm not entirely sold that the question unambiguously means that. Indeed, if the question does intend for you to sketch the region that satisfies the inequality irrespective of what values of z and w are provided (given that they satisfy the conditions), your answer seems to be correct.

So at the end of the day, maybe the question should have just been a bit clearer - saying "sketch the region in terms of z and w" would seem to do the trick. But either way if you interpreted it the way you did in the exam, I can only assume you'd get 2/3 or 3/3 as you've still done all of the correct mathematical working to get to the point - you then just did a little bit of extra work to satisfy a different interpretation of what the question means. Not that I'm an HSC marker or anything so don't hold me to it, but I want to think you'd be fine.

 

[tywebb]

You can just say the gradient is greater than 1 like this:

 

[tywebb]

go to the desmos and add "/yf1efslc4b" after "calculator" in the url, you can see that the region should include y=x by dragging the z slider around.

I like your desmos though.

I don't think it's as hard as has been reported in the media. I just reduces down to an exercise in inequalities.

 

[sam davis hostage]

Okay this is really interesting - I don't think you're correct but you've found something interesting and probably worth discussing.

The first thing to note is that the dotted line in the screenshot is labelled . That means that the point (-1, -1) isn't on the line at all, because exactly as you pointed out, .

But I think the interesting bit is I think you're interpreting the question as "Sketch the region where the inequality holds for all possible values of z, w which satisfy the restriction." However, everyone else seems to have interpreted the question as "Sketch the region where the inequality holds in terms of z, w." I think the way the question is worded, this is more appropriate, just because of the way that z and w seem to be referred to as constants rather than variables, but I'm not entirely sold that the question unambiguously means that. Indeed, if the question does intend for you to sketch the region that satisfies the inequality irrespective of what values of z and w are provided (given that they satisfy the conditions), your answer seems to be correct.

So at the end of the day, maybe the question should have just been a bit clearer - saying "sketch the region in terms of z and w" would seem to do the trick. But either way if you interpreted it the way you did in the exam, I can only assume you'd get 2/3 or 3/3 as you've still done all of the correct mathematical working to get to the point - you then just did a little bit of extra work to satisfy a different interpretation of what the question means. Not that I'm an HSC marker or anything so don't hold me to it, but I want to think you'd be fine.

Thanks, I see my misunderstanding. I incorrectly assumed it meant to sketch the region that would satisfy all z and w, instead of being in terms of z and w. I had drawn my solution, and by comparing graphs I assumed that I had made a mistake with my inequality and not my understanding of the question.

 

[Sam14113]

I don't think it's as hard as has been reported in the media. I just reduces down to an exercise in inequalities.

Agreed, but I think that’s generally the case in HSC. It’s not Putnam - the questions aren’t exceptionally difficult - but we do have quite a few of them for three hours and they make you think. I think the hardest part of the graphing question was realising that the condition given wasn’t actually about the arguments, but instead about it being in the second quadrant. Once you got that, it’s downhill