-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Answer AlarmBell's Questions Thread (1 Viewer)
- Thread starter AlarmBell
- Start date
anomalousdecay
Premium Member
- Joined
- Jan 26, 2013
- Messages
- 5,766
- Gender
- Male
- HSC
- 2013
Suppose polynomial p lies in 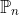 and polynomial q lies in
and polynomial q lies in 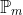 .
.
For a solid proof I would do the following:
Show for cases where n = 1 and m = 1, n = k, m = r.
Then use induction, n = k+1, m = r+1. State that if p and q are both continuous for all complex/real inputs (can't remember which course where you can assume all polynomials are in complex sets) then the composite is also continuous.
Then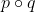 becomes a polynomial that lies in
becomes a polynomial that lies in 
As an engineer I would totally look at it and see what the resultant dimension for the manipulation is for any arbitrary m and n, then skip the proof part.
For b), check the definition for polynomials and mention continuity. You can use the result from part a) to help.
I could be wrong with a few things here as it's been a very long time since I touched this sort of maths.
For a solid proof I would do the following:
Show for cases where n = 1 and m = 1, n = k, m = r.
Then use induction, n = k+1, m = r+1. State that if p and q are both continuous for all complex/real inputs (can't remember which course where you can assume all polynomials are in complex sets) then the composite is also continuous.
Then
As an engineer I would totally look at it and see what the resultant dimension for the manipulation is for any arbitrary m and n, then skip the proof part.
For b), check the definition for polynomials and mention continuity. You can use the result from part a) to help.
I could be wrong with a few things here as it's been a very long time since I touched this sort of maths.
Hey, thanks for your reply! I don't fully get it. Sorry but could you explain further with full working out please?Suppose polynomial p lies inand polynomial q lies in
.
For a solid proof I would do the following:
Show for cases where n = 1 and m = 1, n = k, m = r.
Then use induction, n = k+1, m = r+1. State that if p and q are both continuous for all complex/real inputs (can't remember which course where you can assume all polynomials are in complex sets) then the composite is also continuous.
Thenbecomes a polynomial that lies in
As an engineer I would totally look at it and see what the resultant dimension for the manipulation is for any arbitrary m and n, then skip the proof part.
For b), check the definition for polynomials and mention continuity. You can use the result from part a) to help.
I could be wrong with a few things here as it's been a very long time since I touched this sort of maths.
Hey, thanks for your reply! I don't fully get it. Sorry but could you explain further with full working out please?
Both of these use the intermediate value theorem (IVT).Hey can anyone help me with these 2?

For 7), note that g(0) = f(0) – 0 = f(0), which is in [0, 1], since the range of f is in [0, 1]. If f(0) = 0, we have a suitable c of c = 0.
So suppose g(0) = f(0) is strictly positive instead (this is the only other possibility, since the range of f is [0, 1]). Now, g(1) = f(1) – 1. If f(1) = 1, we can use c = 1. Otherwise, we have f(1) < 1, since range(f) is a subset of [0, 1]. If f(1) < 1, then g(1) = f(1) – 1 < 0. So g(0) > 0 and g(1) < 0. Since g is continuous (being the difference of two continuous functions), it follows by the IVT that for some c in (0, 1), we have g(c) = 0, i.e. f(c) = c. So overall, we have f(c) = c for some c in [0, 1].
----------------
For 8), since we are given that the limit of f(x) as x approaches infinity is -1, there must be an M > 0 such that f(x) is less than distance 1/2 (say) from -1 for all x > M (this follows from the definition of a limit to infinity). Hence for all x > M, we have f(x) < -1/2 < 0. So since f(0) = 1 > 0 and f(x) < 0 for some positive x > M, we have f(c) = 0 for some c in (0, inf), by the IVT (as f is given to be continuous). This proves the result.


