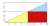
We need to find the area of the colored triangle (image is given below) with coordinates (0, 0), (20, 0), (20, 9). This will mean that the area of the triangle is 90 units^2 since 20*9/2 = 90. However if we follow the steps from b to e we will see the area of the triangle is 90.5.
(b) Show that the yellow (lower) right triangle has area 27.5.
(c) Show that the red rectangle has area 45.
(d) Show that the blue (upper) right triangle has area 18.
(e) Add the results of parts (b), (c), and (d), showing that the area of the colored
region is 90.5.
Question: Why do we get a different result?
(b) Show that the yellow (lower) right triangle has area 27.5.
(c) Show that the red rectangle has area 45.
(d) Show that the blue (upper) right triangle has area 18.
(e) Add the results of parts (b), (c), and (d), showing that the area of the colored
region is 90.5.
Question: Why do we get a different result?


