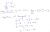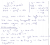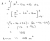Hi! I was stuck on two questions from the Cambridge Mathematics Extension 1 Textbook => Exercise 5G Q14 and Q17.
- I was able to do the graphing and working out but I got the wrong answer from the textbook answers. Could someone help me with worked solutions, so I can see where I went wrong? Thanks!!
View attachment 35590
View attachment 35591
Question 17
Pretty straightforward
Ask yourself, what does the function
=x^{3})
look like?
Once you have that find the zeros in
)
.
Once that is solved step 2
Find x=0 for
)
by subbing x=0 into
)
as
)
is an upward facing parabola that got moved down by 1. Note here you have found a section where
 > g\left(x\right))
.
That is not the end of the story and I assume that is where you had difficulties.
At this point we need to have
=g\left(x\right))
, thus giving us
\left(x-1\right)\left(x-3\right)=\left(x+1\right)\left(x-1\right))
.
Simplifying we will have
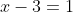
implying
=g\left(x\right))
at
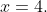
Thus,
 > g\left(x\right))
in the ranges of
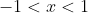
and
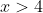
.
part ii
This is where I have a very interesting way of viewing the question. Let me give you a simple question. Suppose we have decided to replace x with 10 so now instead of
\left(x-1\right)\left(x-3\right))
we have
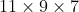
. Pretty self-explanatory.
At this point, we will obtain 693-99 which gives us 594 which simply is
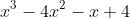
in the range of -1 to 1 noting that
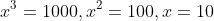
.
The other region is 99-693 which is -594 which when converted to a polynomial is just
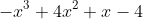
in the range of 1 to 4.
Now we have this in the bag convert them to integrals
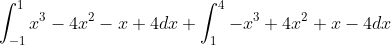
. Solve this on your own. If you need further help or clarification then you can reply here describing what you need help on or what you need clarified.