Argument question help (1 Viewer)

Run hard@thehsc · Dec 4, 2021

I do know that you split up the arguments as arg(z-2) = arg(z) for part (a). But can someone please explain generally the reasoning and methodology behind answering this type of questions? Thanks!

5uckerberg · Dec 4, 2021

Run hard@thehsc said:
View attachment 34413
I do know that you split up the arguments as arg(z-2) = arg(z) for part (a). But can someone please explain generally the reasoning and methodology behind answering this type of questions? Thanks!

Okay here is the general guideline. Think of the sketches as a walk from the start to the end. Albeit from the numerator to the denominator.
Next, the objective is to set up your Argand diagram and flip that argand diagram so that if you are going forwards positive numbers go on the top and if you are going backwards negative numbers go to the top.
Now look at the arc of the circle specified.
This will tell us that you ought to start at your destination and there your knowledge of bearings should guide you on what the arc will look like and then for the orientation it is 180 degrees minus the bearing given in the question.

Run hard@thehsc · Dec 4, 2021

oh ok. could you please kinda elaborate on the positive and negative numbers part?

5uckerberg · Dec 4, 2021

Run hard@thehsc said:
oh ok. could you please kinda elaborate on the positive and negative numbers part?

The rest follows the same idea.

CM_Tutor · Dec 5, 2021

$\arg{\left(\cfrac{z-1}{z+3}\right)} = \cfrac{\pi}{6} \quad \implies \quad \arg{(z-1)} - \arg{(z+3)} = \cfrac{\pi}{6}$

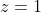
Consider the vector from $z = 1$ to some point in the first quadrant so that the angle between the vector and the real axis in the positive direction is $\alpha$ , an acute angle. This is the vector $z - 1$ and points in the direction $\arg{(z - 1)} = \alpha$ .

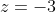
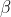
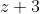
Consider also the vector from $z = -3$ to some point in the first quadrant so that the angle between the vector and the real axis in the positive direction is $\beta$ , an acute angle. This is the vector $z + 3$ and $\arg{(z + 3)} = \beta$ .

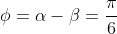
We now seek the locus where $\phi = \alpha - \beta = \cfrac{\pi}{6}$ , and this angle is formed where the two vectors meet.

The locus is a semi-circle if $\phi = \cfrac{\pi}{2}$ , in which case $A\ (z = 1)$ ) and $B\ (z = -3)$ define the end points of the diameter.
It is a minor arc when $\cfrac{\pi}{2} < \phi < \pi$
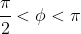
It is a major arc when $0 < \phi < \cfrac{\pi}{2}$
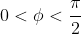
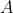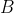In any of these cases, the two points $A$ and $B$ define a chord of the circle.
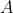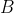Note that, in each case, the points $A$ and $B$ are excluded from the locus as each produces an argument of the complex number 0, which is undefined.

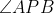
The loci are parts of a circle as, if $P$ is a point on the locus, the $\angle{APB}$ is fixed because angles standing on the same chord or arc must all be equal.

CM_Tutor · Dec 6, 2021

Further, if the placement of $z$ in the first quadrant doesn't work, you need to find a suitable placement. For example,

$\arg{\cfrac{z+2}{z - 1}} = \cfrac{\pi}{4}$

We need $\arg{(z + 2)} = \alpha$ , the direction of the vector from -2 to $z$ , to be $-\pi < \alpha < 0$ .
Drawing the ray for this vector, we position $z$ on it so that the vector from 1 to $z$ , with direction $\beta = \arg{(z - 1)}$ where $-\pi < \beta < \alpha$ , results in the angle between the vectors being $0 < \alpha - \beta = \cfrac{\pi}{4}$ .
Our locus is then the major arc of the circle with
- the real axis between $z = -2$ and $z = 1$ as a chord
- its centre can be deduced geometrically to be at $z = -\cfrac{1}{2} - \cfrac{3i}{2}$ .
The Cartesia equation of the locus will be

$\left(x + \cfrac{1}{2}\right)^2 + \left(y + \cfrac{3}{2}\right)^2 = \cfrac{9}{2} \quad \text{for $y < 0$}$

or, equivalently

$(2x + 1)^2 + (2y + 3)^2 = 18 \quad \text{for $y < 0$}$

Derived algeraically, we start by letting $z = x + iy$ and proceed:

$\begin{align*} \arg{\left(\cfrac{z + 2}{z-1}\right)} &= \cfrac{\pi}{4} \\ \arg{[(x + 2) + iy]} - \arg{[(x - 1) + iy]} &= \cfrac{\pi}{4} \qquad \text{substituting $z = x + iy$ and rearranging} \\ \tan^{-1}{\left(\cfrac{y}{x+2}\right)} - \tan^{-1}{\left(\cfrac{y}{x-1}\right)} &= \cfrac{\pi}{4} \\ \cfrac{\tan{\left[\tan^{-1}{\left(\cfrac{y}{x+2}\right)}\right]} - \tan{\left[\tan^{-1}{\left(\cfrac{y}{x-1}\right)}\right]}}{1 + \tan{\left[\tan^{-1}{\left(\cfrac{y}{x+2}\right)}\right]} \times \tan{\left[\tan^{-1}{\left(\cfrac{y}{x-1}\right)}\right]}} &= \tan{\cfrac{\pi}{4}} \qquad \text{on expanding $\tan{(\theta - \phi)}$} \\ \cfrac{\cfrac{y}{x+2} - \cfrac{y}{x-1}}{1 + \cfrac{y}{x+2} \times \cfrac{y}{x-1}} &= 1 \\ \cfrac{y(x - 1) - y(x + 2)}{(x - 1)(x + 2) + y^2} &= 1 \\ x^2 + x + y^2 + 3y &= 2 \\ \left(x^2 + x + \cfrac{1}{4}\right) + \left(y^2 + 3y + \cfrac{9}{4}\right) &= 2 + \cfrac{1}{4} + \cfrac{9}{4} \\ \left(x + \cfrac{1}{2}\right)^2 + \left(y + \cfrac{3}{2}\right)^2 &= \cfrac{9}{2} \end{align*}$

I am leaving it for you to determine where in this algebraic derivation the restrictions on the locus arise. One reason for favouring a geometric approach over an algebraic one is that the exclusions are more obvious.

Argument question help (1 Viewer)

Run hard@thehsc

Well-Known Member

5uckerberg

Well-Known Member

Run hard@thehsc

Well-Known Member

5uckerberg

Well-Known Member

Attachments

CM_Tutor

Moderator

CM_Tutor

Moderator

Users Who Are Viewing This Thread (Users: 0, Guests: 1)