asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,225
- Gender
- Undisclosed
- HSC
- 2012
4c
i) If^k) , where c>0, k>0, k=/=1, show y has a single stationary value between x=0 and x=c, and show that this stationary value is a maximum if 0<k<1 and a minimum if k>1. (3)
, where c>0, k>0, k=/=1, show y has a single stationary value between x=0 and x=c, and show that this stationary value is a maximum if 0<k<1 and a minimum if k>1. (3)
ii) Hence show that if a>0, b>0, a=/=b, then^k) if 0<k<1 and
if 0<k<1 and ^k) if k>1 (4)
if k>1 (4)
I've done i)
^{k-1}=0) for stationary points, ends up
for stationary points, ends up 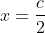
For k<1, k-1<0, so cc down, rel max. For k>1, k-1>0, so cc up, rel min.
ii)
At^k)
If maximum, then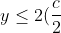^k)
If minimum,...
Don't know where to go
Any help is greatly appreciated.
i) If
ii) Hence show that if a>0, b>0, a=/=b, then
I've done i)
For k<1, k-1<0, so cc down, rel max. For k>1, k-1>0, so cc up, rel min.
ii)
At
If maximum, then
If minimum,...
Don't know where to go
Any help is greatly appreciated.
