Given the coordinates
)
and
)
you know that the distance
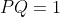
and you know that
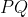
must be the diagonal of the square (it can't be a side as
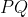
is horizontal but the sides of the square have gradients of
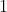
and
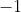
).
Now, for any square of side length

with diagonal length
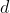
, Pythagoras' Theorem gives us that
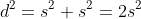
, and since the area of a square is
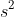
, we can conclude that:

and since we know here that
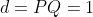
, it follows that:

If you were not told that the two normals and tangents enclosed a square, you could deduce it geometrically as follows:
- The angle between the tangent at
 and the normal at
and the normal at  is a right angle from the definition of a normal at a point on a curve as the line perpendicular to the tangent at that point.
is a right angle from the definition of a normal at a point on a curve as the line perpendicular to the tangent at that point.
- It follows that the angle between the tangent at
 and the normal at
and the normal at 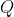 is also a right angle
is also a right angle
- We know that the tangents at
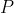 and
and 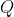 have gradients of
have gradients of  and
and  , respectively, and since
, respectively, and since  , these two tangents are perpendicular
, these two tangents are perpendicular
- So, our quadrilateral is either a square or a rectangle (as all four of its angles are 90 degrees)
- The midpoint of
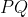 is at
is at ) , and it must also be the midpoint of the other diagonal,
, and it must also be the midpoint of the other diagonal, 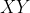 , whether the quadrilateral is a square or a rectangle
, whether the quadrilateral is a square or a rectangle
- If the shape is a square, the diagonals must be perpendicular, and since
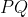 is horizontal, that would make
is horizontal, that would make 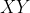 vertical, so let's try for
vertical, so let's try for 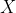 and
and 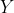 to lie on
to lie on 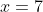
- Now, the tangent at
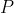 has a gradient of 1 and so any change in
has a gradient of 1 and so any change in  will be accompanied by the same change in
will be accompanied by the same change in 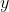 - that is
- that is 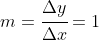
- Starting from
 , we need
, we need  to move to
to move to  , making
, making  , and putting
, and putting  at
at  = \Big(7\cfrac{1}{2} - \cfrac{1}{2}, 3\cfrac{1}{4} - \cfrac{1}{2}\Big) = \Big(7, 2\cfrac{3}{4}\Big))
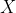 does lie on the tangent at
does lie on the tangent at 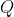 (evident since that tangent has gradient -1 and so a
(evident since that tangent has gradient -1 and so a  requires
requires  , making the shift from
, making the shift from 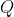 to
to 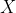 :
:  = \Big(7, 2\cfrac{3}{4}\Big)) as required
as required- We immediately know the coordinates of
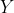 are
are ) because
because 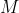 is the midpoint of
is the midpoint of 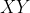 , but this could also be established by a similar method using the two normals
, but this could also be established by a similar method using the two normals
- We have confirmed that
 is a square as
is a square as  (as
(as 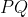 is horizontal and
is horizontal and 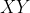 is vertical)
is vertical)
- We have the area as half the square of the diagonal, or we could show that all four sides have the same length
) and then say that the area is
and then say that the area is ^2 = \cfrac{1}{2})
