Re: Year 11 Mathematics 3 Unit Cambridge Question & Answer Thread
 \Big{]}_{x=a} ^{x=b}$, where $y(x)$ is the function of $x$, in our case $x\mathrm{e}^x$.$)
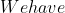
 \mathrm{e}^x \quad (\text{from your working}) \\ &= x\mathrm{e}^x + \mathrm{e}^x \\ \Rightarrow x\mathrm{e}^x &= \frac{\mathrm{d}y}{\mathrm{d}x} - \mathrm{e}^x \\ \Rightarrow \int _0 ^2 x \mathrm{e}^x \text{ d}x &= \int_0 ^2 \left( \frac{\mathrm{d}y}{\mathrm{d}x} - \mathrm{e}^x \right) \text{ d}x \quad (\text{integrating both sides from 0 to 2}) \\ &= \Big{[}y(x) - \mathrm{e}^x \Big{]}_{0} ^{2} \quad (\text{using the Fundamental Theorem of Calculus}) \\ &= \Big{[}x\mathrm{e}^x - \mathrm{e}^x \Big{]}_{0} ^{2} \quad (\text{as }y(x) = x\mathrm{e}^x) \\ &= \left(2 \mathrm{e}^2 - \mathrm{e}^2 \right) - \left(0-1 \right) \\ &= \mathrm{e}^2 +1. \end{align*}$$)
Question 9, Chapter 13C of Year 11 Maths 3U Cambridge.
I found the first part being dy/dx=(x+1)e^x but the I have no idea how to do the integration from there :/


