Umm...doesn't that lead an inequality with an unknown in the denominator which is beyond the 2u course?
This is what I get without requiring an unknown in the denominator.
Suppose that
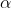
and
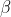
are the roots where
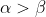
. We are given that

Sum of roots:

Product of roots:

But
^2 \\\\= \alpha^2 - 2\alpha\beta + \beta^2 \\\\= \alpha^2 + 2\alpha\beta + \beta^2 - 4\alpha\beta \\\\= (\alpha + \beta)^2 - 4\alpha\beta \\\\ = \dfrac{25}{k^2} - \dfrac{24}{k})
Since

then
^2 < 1)
Substituting the result we get

Note that since the denominator is always non-negative, the sign of the inequality is unchanged (whereas in your case you need to deal with cases where k is positive/negative etc).
Looking at the left inequality we immediately get the upper bound.

Looking at the right inequality.
(k - 1) > 0\\\\\Rightarrow k < -25 $ or $ k > 1)
Tehnically speaking, putting the inequalities together we should get
 Missing a solution set haya!
Missing a solution set haya! 


