-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Complex number calculator necessary for maths ext 2? (1 Viewer)
- Thread starter Beca-W
- Start date
DatAtarLyfe
Booty Connoisseur
- Joined
- Mar 10, 2015
- Messages
- 1,801
- Gender
- Female
- HSC
- 2016
No. If you need a cal to do basic complex numbers you shouldn't be doing 4u
pikachu975
Premium Member
It's not really necessary but I guess you can check your complex number arithmetic or mod-arg conversions.Hey everyone,
I'm just wondering whether it would be advantageous to get a complex number calculator for 4U maths?
Thanks!
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Maybe if you're relying on it to do them. But what's the harm in getting one to check your answer so that you can guarantee those marks?No. If you need a cal to do basic complex numbers you shouldn't be doing 4u
It might be advantageous for you to easily get those complex number calculations done without spending too much time on the algebra side, but in the long-run it could potentially have a negative outcome of your algebraic skills. I would just stay on the same level as the other students in your class (assuming they don't all have complex number calculators) just to get used to the time it takes to do some complex number calculations, since time management will be very important during an exam.Hey everyone,
I'm just wondering whether it would be advantageous to get a complex number calculator for 4U maths?
Thanks!
D94
New Member
- Joined
- Oct 5, 2011
- Messages
- 4,419
- Gender
- Male
- HSC
- N/A
Because a calculator is only as good as your input. GIGOMaybe if you're relying on it to do them. But what's the harm in getting one to check your answer so that you can guarantee those marks?
There are other tests to determine the correctness of your solution. It's more important for a student to learn these than to use a calculator since you won't have access to those calculators in an exam.
pikachu975
Premium Member
The fx 100 AU plus is allowed in exams and it's a complex number calculator though.Because a calculator is only as good as your input. GIGO
There are other tests to determine the correctness of your solution. It's more important for a student to learn these than to use a calculator since you won't have access to those calculators in an exam.
D94
New Member
- Joined
- Oct 5, 2011
- Messages
- 4,419
- Gender
- Male
- HSC
- N/A
I meant in general on the reliance of calculators.The fx 100 AU plus is allowed in exams and it's a complex number calculator though.
Silly Sausage
Well-Known Member
- Joined
- Dec 8, 2014
- Messages
- 594
- Gender
- Male
- HSC
- 2014
Quite handy in certain situations only e.g. finding the complex roots of a quadratic equation, won't give you much of an advantage but still comes useful sometimes.
Curious as to how you would do this? (on the fx 100 au plus)?Quite handy in certain situations only e.g. finding the complex roots of a quadratic equation, won't give you much of an advantage but still comes useful sometimes.
pikachu975
Premium Member
I have the complex number calculator it's not as useful as it seems
marxman
Member
- Joined
- Jan 12, 2016
- Messages
- 51
- Gender
- Male
- HSC
- 2016
I used mine quite a bit and in reality there is no serious disadvantage to owning one. It can help you get 1 mark questions in a matter of seconds and also check your arithmetic on any yucky computations.
From a competitive perspective, if it's allowed to be used then you can assume other people will use it, and these people will have the advantage of being able to do calculations faster than you. It's unnecessary to put yourself at this kind of disadvantage (unless you are an absolute complex arithmetic genius).
From a competitive perspective, if it's allowed to be used then you can assume other people will use it, and these people will have the advantage of being able to do calculations faster than you. It's unnecessary to put yourself at this kind of disadvantage (unless you are an absolute complex arithmetic genius).
dan964
what
For those who have the fx82AU or fx100au, you can use the Pol() and Rec() functions (learn how to use them), to convert a complex number from x+iy form
to polar form. Just simply convert the number from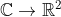
So write Pol(x,y) gives you the modulus and the angle which are stored to X and Y variables on your calculator respectively. (Modulus is stored as the X variable and as the Ans key, you can then square it to find what it is the squareroot of; and for the Angle typing in Y and then pressing the relevant key can convert it into degrees and minutes (if calculator is set to such).
To go the other way put Rec(|z|, argz), gives you x and y, which are stored under X and Y variables.
For complex roots, remember that if you are solving a quadratic equation with real coefficients, both the root and its conjugate are roots. The easier way to find quadratic roots is to simply use the quadratic formula.
Firstly compute (the discriminate) if this is negative then you have two complex roots...
(the discriminate) if this is negative then you have two complex roots...
So then if that is the case, if you can complete the square to the form^2 + b^2) , then the complex number a+ib and a-ib are roots. (This is derivated from
, then the complex number a+ib and a-ib are roots. (This is derivated from (x-a-ib) =(x-a)^2-(ib)^2)
to polar form. Just simply convert the number from
So write Pol(x,y) gives you the modulus and the angle which are stored to X and Y variables on your calculator respectively. (Modulus is stored as the X variable and as the Ans key, you can then square it to find what it is the squareroot of; and for the Angle typing in Y and then pressing the relevant key can convert it into degrees and minutes (if calculator is set to such).
To go the other way put Rec(|z|, argz), gives you x and y, which are stored under X and Y variables.
For complex roots, remember that if you are solving a quadratic equation with real coefficients, both the root and its conjugate are roots. The easier way to find quadratic roots is to simply use the quadratic formula.
Firstly compute
So then if that is the case, if you can complete the square to the form
Last edited:
pikachu975
Premium Member
Just a question unrelated, but about square roots:For those who have the fx82AU or fx100au, you can use the Pol() and Rec() functions (learn how to use them), to convert a complex number from x+iy form
to polar form. Just simply convert the number from
So write Pol(x,y) gives you the modulus and the angle which are stored to X and Y variables on your calculator respectively. (Modulus is stored as the X variable and as the Ans key, you can then square it to find what it is the squareroot of; and for the Angle typing in Y and then pressing the relevant key can convert it into degrees and minutes (if calculator is set to such).
To go the other way put Rec(|z|, argz), gives you x and y, which are stored under X and Y variables.
For complex roots, remember that if you are solving a quadratic equation with real coefficients, both the root and its conjugate are roots. The easier way to find quadratic roots is to simply use the quadratic formula.
If you can complete the square to the form, then the complex number a+ib and a-ib are roots. (This is derivated from
(x-a-ib) =(x-a)^2-(ib)^2)
When square rooting a complex number e.g. 8 + 6i
So we use the form a^2 +2abi - b^2
sqrt [3^2 - 1^2 + 2*3*i] = +/- (3+i)
Is this quick method allowed for like 2-3 markers for square rooting or is it only for multiple choice? Is it allowed or do we have to do the long method:
a^2 + 2abi - b^2 = 8 + 6i
Equating real and imaginary parts....
Thanks!
In other words, inspection. Should be fine as long as it's clear what you did.Just a question unrelated, but about square roots:
When square rooting a complex number e.g. 8 + 6i
So we use the form a^2 +2abi - b^2
sqrt [3^2 - 1^2 + 2*3*i] = +/- (3+i)
Is this quick method allowed for like 2-3 markers for square rooting or is it only for multiple choice? Is it allowed or do we have to do the long method:
a^2 + 2abi - b^2 = 8 + 6i
Equating real and imaginary parts....
Thanks!
Last edited:
dan964
what
Inspection works with integers/simple fractions.Just a question unrelated, but about square roots:
When square rooting a complex number e.g. 8 + 6i
So we use the form a^2 +2abi - b^2
sqrt [3^2 - 1^2 + 2*3*i] = +/- (3+i)
Is this quick method allowed for like 2-3 markers for square rooting or is it only for multiple choice? Is it allowed or do we have to do the long method:
a^2 + 2abi - b^2 = 8 + 6i
Equating real and imaginary parts....
Thanks!
