This is formally known as the triangle inequality however indeed it is quite logical.
Can I not establish the fact that the sum of any 2 sides of a triangle are greater than the third side?
Now lets apply this to our complex plane.
I advise you to draw this out as I say it so you can understand it:
Take the 2 complex numbers z1 and z2. If we add them, by vector addition we create a parallelogram as you know to make z1+z2 (Or we make a triangle using head-tail method)
Now look at the diagonal, it represents z1+z2. This diagonal splits our parrallellogram into 2 triangles. Take a look at one of them. Look at the length of the sides.
The diagonal side is | z1 +z2 |
One of the sides is | z1 |
The other is | z2 | (by opposite sides of parrallelogram being same size)
Apply the triangle inequality logic here.

Done.
When are they equal? Imagine it out like the parrallegram, z1 and z2 must be on the same LINE right?
=arg(z_2) )
It is important to notice that it is NOT:
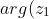=arg(z_2) + \pi k )
