goobi
Member
- Joined
- Oct 6, 2010
- Messages
- 196
- Gender
- Male
- HSC
- 2012
Find the equations of the tangent and normal to the ellipse  at the point
at the point ) .
.
If the tangent meets the x-axis at P and the normal meets the y-axis at Q, show that PQ touches the ellipse.
Edit:
So I've found the equation of the tangent:
 ......(1)
......(1)
And the equation of the normal:
 ......(2)
......(2)
Substituting y=0 into (1), P is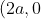)
Substituting x=0 into (2), Q is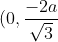)
Gradient of PQ =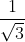
Therefore, equation of PQ is: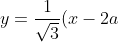)
And I have no idea what to do next...
Any help would be appreciated
If the tangent meets the x-axis at P and the normal meets the y-axis at Q, show that PQ touches the ellipse.
Edit:
So I've found the equation of the tangent:
And the equation of the normal:
Substituting y=0 into (1), P is
Substituting x=0 into (2), Q is
Gradient of PQ =
Therefore, equation of PQ is:
And I have no idea what to do next...
Any help would be appreciated
Last edited:
