Fus Ro Dah
Member
- Joined
- Dec 16, 2011
- Messages
- 247
- Gender
- Male
- HSC
- 2013
Here is a neat result.
Prove that for all natural numbers N,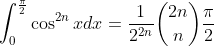
Prove that for all natural numbers N,
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Haha although I do appreciate your enthusiasm, remember that this thread is for MX1. Your question is more suitable for MX2 students. There are a few ways of doing it though (I'm saying this because many MX2 students lurk here).Here is a neat result.
Prove that for all natural numbers N,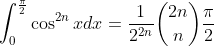
Yep, this is Method #1 that I had. Try doing it Method 2.http://community.boredofstudies.org/showthread.php?t=284850
I already proved this in this thread, but replace cos with sin (it's the same result anyway as the two integrals are equal).
I'll give it a go tomorrow afternoon since my 4U test will be over (ie I'd rather get some sleep tonight).Yep, this is Method #1 that I had. Try doing it Method 2.
It may very well be a past HSC question, problems like these are very commonly asked. Proving Trigonometric Series by means of Complex Numbers and expressions.Wasn't this a past paper question?
If I remember what i did the first time i tried this question, for carrotsticks' method #2, you go and prove:
i. z^n + z^-n = 2cos(ntheta) by de moivre's theorem & some manipulation
ii. use this to then expand (2cos(theta))^2n = some binomial mess which i won't even attempt to type
iii. and to prove that the integral in question is true, you sub in the result of ii. and all of the cos((2n + k)theta) bits integrate into something like sin((2n + k)theta)/(2n + k), which all cancel out anyway because sin(2k pi/2) = 0 for some integer k
hence the remaining term of the expansion will be the RHS of the intergal
Did you mean for negative limits? I don't fully understand what you're saying.It helps having a past paper book within arm's reach lol.
Now, what happens to the integral in question for negative numbers?
Although de moivre's theorem extends to negatives, the binomial expansion is radically different (assuming it exists)
It's also done in second year in Analysis.Ahh, of course. I forgot about turning it into a sec-based problem, but I am unfamiliar with the relationship between integration and convergence/divergence. I was too busy trying to think of some way I could express this new integral in terms of the original.
I wish this damn HSC would hurry up and finish so I can go learn this all in uni. This level of Series, Sequences and Integration is in 1st year uni, isn't it?
we have those people at uni tooI can't be the only one who has/had their teachers tell them to shut up in class because they were rambling on and on about tertiary-level maths.

