Carrot, can you teach me how to do contour integration, looks like a pretty cool technique.
For example, I'm doing this bad ass nasty little integral and I couldn't continue because I have a contour integral:
}{1+(x)^{2}}dx)
}{(x+i)(x-i)}dx=1/2 \int_{-\infty}^{\infty} \frac{\cos(x)}{(x+i)(x-i)}dx)
then consider the contour integral:
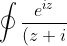(z-i)}dz)
where the contour is the half-disc in the upper half plane, then just use the Residue Theorem.
I think this is really interesting, I never thought integration gets any more advanced =)
For example, I'm doing this bad ass nasty little integral and I couldn't continue because I have a contour integral:
then consider the contour integral:
where the contour is the half-disc in the upper half plane, then just use the Residue Theorem.
I think this is really interesting, I never thought integration gets any more advanced =)
Last edited: