-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Differentiating harder inverse trig (1 Viewer)
- Thread starter Danmiff
- Start date
K
khorne
Guest
You can use the chain rule, and in this case, make a substitution u = rt(x):
so:
d/dx arcsin(x^.5) = d arcsin(u)/du *du/dx (d/dx arcsin(u)/du = 1/rt[1-u] )
=d/dx rt(x)/rt(1-x) = 1/2rt(1-x) rt(x)
so:
d/dx arcsin(x^.5) = d arcsin(u)/du *du/dx (d/dx arcsin(u)/du = 1/rt[1-u] )
=d/dx rt(x)/rt(1-x) = 1/2rt(1-x) rt(x)
lychnobity
Active Member
- Joined
- Mar 9, 2008
- Messages
- 1,292
- Gender
- Undisclosed
- HSC
- 2009
EDIT:
Last edited:
scardizzle
Salve!
it' s kind of like the chain rule:
d (sin^-1 f(x)) = 1/(1- f(x)^2)^1/2 x f'(x)
dx
d (sin^-1 f(x)) = 1/(1- f(x)^2)^1/2 x f'(x)
dx
tom.evans.15
New Member
- Joined
- Aug 31, 2008
- Messages
- 7
- Gender
- Male
- HSC
- 2010
Correct me if im wrong, but it IS the chain rule right?it' s kind of like the chain rule
y=asin(f(x)) is in the form y=g(f(x)) where g(x) = asinx
therefore dy/dx = g'(f(x)) * f'(x)
so d/dx(asinf(x)) = (1/sqrt(1-(f(x)^2))*(f'(x))
and please, correct me if im wrong
K
khorne
Guest
Yes, you're right, but 3 people beat you to it =]
tom.evans.15
New Member
- Joined
- Aug 31, 2008
- Messages
- 7
- Gender
- Male
- HSC
- 2010
Oh well. Doesn't matter...Yes, you're right, but 3 people beat you to it =]
tbh, the explanation was more for my own sake rather than OPs or anyone elses...
but i'm right, so i feel good now
scardizzle
Salve!
well i only said it was kinda of like the chain rule because my idea of the chain rule is
d(f(x)^n) = n f(x)^n-1 . f'(x)
dx
so i guess maybe i should have said this was a different version of the chain rule
d(f(x)^n) = n f(x)^n-1 . f'(x)
dx
so i guess maybe i should have said this was a different version of the chain rule
Last edited:
untouchablecuz
Active Member
- Joined
- Mar 25, 2008
- Messages
- 1,693
- Gender
- Male
- HSC
- 2009
imo
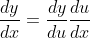
is the easiest/most useful form of the chain rule
is the easiest/most useful form of the chain rule
