Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Difficult induction question, or maybe I'm just missing something simple? (1 Viewer)
- Thread starter yanujw
- Start date
just did it pretty simpleRequired to prove:is divisible by 8
idk what ur having a problem with tho but make sure u prove the stuff that doesn't get multiplied by 8 is divisible by 8 the
I tried it and couldn't do it either, thought I was ok at induction but apparently not. My working is below if someone is willing to tell me where I went wrong. Also sorry but idk how to use latex
Show true when n=1
= 3^(2x2) - 1
= 3^4 - 1
=80
=8x10 therefore true for n=1
Assume n=k
3^(2k)^2 -1
= 3^(4k^2) -1 = 8P (Where P is an integer)
Show true for when n=k+1
3^[2(k+1)]^2 -1 = 8Q (Where Q is an integer)
LHS = 3^(2k+2)^2 -1
=3^(4k^2+8K+4) -1
=3^(4k^2) x 3^(8k) x 3^(4) -1
= 8P x 81 x 3^(8k) (using line from assume n=k)
??? Idk where to go from here
Show true when n=1
= 3^(2x2) - 1
= 3^4 - 1
=80
=8x10 therefore true for n=1
Assume n=k
3^(2k)^2 -1
= 3^(4k^2) -1 = 8P (Where P is an integer)
Show true for when n=k+1
3^[2(k+1)]^2 -1 = 8Q (Where Q is an integer)
LHS = 3^(2k+2)^2 -1
=3^(4k^2+8K+4) -1
=3^(4k^2) x 3^(8k) x 3^(4) -1
= 8P x 81 x 3^(8k) (using line from assume n=k)
??? Idk where to go from here
careful the 2 isn't squared just do it again and u shud end up withI tried it and couldn't do it either, thought I was ok at induction but apparently not. My working is below if someone is willing to tell me where I went wrong. Also sorry but idk how to use latex
Show true when n=1
= 3^(2x2) - 1
= 3^4 - 1
=80
=8x10 therefore true for n=1
Assume n=k
3^(2k)^2 -1
= 3^(4k^2) -1 = 8P (Where P is an integer)
Show true for when n=k+1
3^[2(k+1)]^2 -1 = 8Q (Where Q is an integer)
LHS = 3^(2k+2)^2 -1
=3^(4k^2+8K+4) -1
=3^(4k^2) x 3^(8k) x 3^(4) -1
= 8P x 81 x 3^(8k) (using line from assume n=k)
??? Idk where to go from here
Not gonna lie, you psyched me out by saying it was "simple", because after investing all my willpower over figuring out how to rearrangeat which point u just proveis divisible by 8 (i did it via mathematical induction)
I have to add though, this is a rather unique induction problem. Most MX1 induction problems I do on autopilot, this is the first one that's made me think in a bit.
i'm sure there's an easier way i just wasn't bothered to figure it out so i just did induction againNot gonna lie, you psyched me out by saying it was "simple", because after investing all my willpower over figuring out how to rearrangesuch that it is in the form
for all integers M I resorted to using a second case of induction like you did. If there is an easier method to this, I'd love to hear it because it's beyond me at the moment.
I have to add though, this is a rather unique induction problem. Most MX1 induction problems I do on autopilot, this is the first one that's made me think in a bit.
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 561
- Gender
- Male
- HSC
- 2018
I think for this one once you get to the n=k+1 step I reckon one can try -f(k)) which should give us
which should give us ^{2}}-3^{2k^{2}}) . Next, this becomes
. Next, this becomes =(8B+1)(2)(...)=8B(2)(...)+2(...)) where ... will give us something that is divisible by 8. The (2) part comes from (3-1)(...) for
where ... will give us something that is divisible by 8. The (2) part comes from (3-1)(...) for 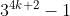
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 561
- Gender
- Male
- HSC
- 2018
Since all of you have seen the mathematical induction question being solved. I will now present you the following.
Prove by mathematical induction that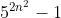 is divisible by 4?
is divisible by 4?
Prove by mathematical induction that
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 561
- Gender
- Male
- HSC
- 2018
I was meant to give the students a little test to see if they have learnt how to work out a similar problem from your solution. Sorry for the misinterpreted message.Can use same approach.
^2} - 1 = 25^{(k+1)^2} - 1 = 25^{k^2 + 2k + 1} - 1 = 25^{2k+1}(25^{k^2} - 1 + 1) -1)
For I believe that students will gain the greatest satisfaction when they do a similar question by themselves after looking at the scaffold from an example.
Last edited:
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 561
- Gender
- Male
- HSC
- 2018
I know what we can do. Edit your work and put it under spoiler and just name it answer or solution that should stop them from looking.My apologies!!!
Now students: please don't look at my solution until you have made an honest attempt.
Eg
"Solution to induction question"
Not gonna lie, you psyched me out by saying it was "simple", because after investing all my willpower over figuring out how to rearrangesuch that it is in the form
for all integers M I resorted to using a second case of induction like you did. If there is an easier method to this, I'd love to hear it because it's beyond me at the moment.
I have to add though, this is a rather unique induction problem. Most MX1 induction problems I do on autopilot, this is the first one that's made me think in a bit.
3^(4k+2) - 1just did it pretty simple
idk what ur having a problem with tho but make sure u prove the stuff that doesn't get multiplied by 8 is divisible by 8 thestuff
=(3^(2k+1)-1)(3^(2k+1)+1)
3^(2k+1)= odd number.
(3^(2k+1)-1) = even
(3^(2k+1)+1) = even
For any four consecutive numbers,
there are two even, and two odd numbers, there must also be one even number that is a multiple of 4.
therefore 4x2, divisible by 8.
alternatively,3^(4k+2) - 1
=(3^(2k+1)-1)(3^(2k+1)+1)
3^(2k+1)= odd number.
(3^(2k+1)-1) = even
(3^(2k+1)+1) = even
For any four consecutive numbers,
there are two even, and two odd numbers, there must also be one even number that is a multiple of 4.
therefore 4x2, divisible by 8.
3^(4k+2) - 1
use x^n-y^n factorisation with 9^(2k+1)-1
to get (8)(....)
3^(4k+2) - 1
=(3^(2k+1)-1)(3^(2k+1)+1)
3^(2k+1)= odd number.
(3^(2k+1)-1) = even
(3^(2k+1)+1) = even
For any four consecutive numbers,
there are two even, and two odd numbers, there must also be one even number that is a multiple of 4.
therefore 4x2, divisible by 8.
both work for the question itself. don't even need induction lmao.alternatively,
3^(4k+2) - 1
use x^n-y^n factorisation with 9^(2k+1)-1
to get (8)(....)
laterz laterz
Well-Known Member
- Joined
- Jul 23, 2020
- Messages
- 471
- Gender
- Male
- HSC
- 2021
titleboth work for the question itself. don't even need induction lmao.
As an afterthought, students may wish to note, in regard to divisibility problems in Proof by Induction:
(x^{n-1} + x^{n-2} + \cdots + x^2 + x + 1) $ for n $ \ge 1\\ \\ 3^{2n^2} - 1 = 9^{n^2} - 1 = (9-1)(9^{n^2 -1} + 9^{n^2-2} + \cdots + 9^2 + 9 + 1) )
Therefore immediately, divisible by 8. Similarly:
(25^{n^2 -1} + 25^{n^2 -2} + \cdots + 25^2 + 25 + 1))
and therefore immediately divisible by 24, as well a 2, 4, 6, 8, & 12.
So Proof by Induction is for such problems, more long-winded. But a good exercise to develop your Proof by Induction skills.
Therefore immediately, divisible by 8. Similarly:
and therefore immediately divisible by 24, as well a 2, 4, 6, 8, & 12.
So Proof by Induction is for such problems, more long-winded. But a good exercise to develop your Proof by Induction skills.
Last edited:
sso
Member
- Joined
- Apr 4, 2021
- Messages
- 88
- Gender
- Male
- HSC
- 2022
Required to prove:is divisible by 8
where did you get this question from?
yanujw
Well-Known Member
- Joined
- May 23, 2020
- Messages
- 338
- Gender
- Male
- HSC
- 2022
I was experimenting with trying to make difficult questions for my own practice and then found that this seemed to work. But then I struggled to prove it lol.where did you get this question from?
