RealiseNothing
what is that?It is Cowpea
Re: The Nonsense Thread
You know the usual matrix equation:
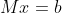
Now the whole idea behind eigenvalues/eigenvectors is to move everything in straight lines as this is the easiest way to do things (just think intuitively about this).
So we want the matrix M to "move" the vector v in straight lines essentially, and so our equation should instead be in the form:
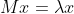
Where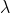
is just some scalar.
Now we call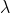 an eigenvalue of M as it is the "scale" that M moves the vector by. This vector being moved is the eigenvector of 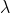associated with M (as different eigenvalues will have different corresponding eigenvectors).
Our first objective is to find the eigenvalues (find eigenvalues first, find eigenvectors second). To do this we re-arrange the matrix equation:
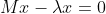
Note this is the zero vector.
 x = 0)
Also note we multiplied the scalar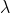 by the identity matrix as 
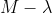is meaningless (we want to subtract two vectors, not a scalar from a vector).
Now how do we find the values of?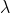
Well we first notice something about)
. If this matrix is invertible, then we get:
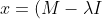^{-1} 0)
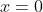
But by definition the eigenvector can never be the zero vector. So we make the observation:
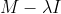is not invertible.
What does this mean? Remember what we learnt about determinants. If something is not invertible, then the determinant must be zero!
So to find eigenvalues we solve:
 = 0)
This will always give us some polynomial of degree equal to rows and columns of M, known as the characteristic polynomial of M. This polynomial will also be in terms of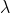. All that is left for us to do is solve this polynomial and we get the values of 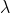, that is, we get the eigenvalues! We can also note here that the amount of distinct eigenvalues can never exceed the degree of the characteristic polynomial, and hence can never exceed the rows/columns of M.
Now we have our eigenvalues, we find our eigenvectors. This is as simple as just solving the original matrix equation:
x = 0)
Once this is solved, we usually get a solution which is a set in terms of a parameter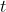
. This gives us the vector space of all eigenvectors. This is just the general solution in terms of 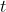for our eigenvectors. Substitute in values of 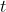and you get your eigenvectors.
Now we know the eigenvalues and eigenvectors we can do some cool things with them. For example, diagonalisation (spelling?). This is basically making it easier to evaluate certain operations on matrixes, i.e.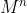
. We use the following form:
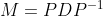
This is a pretty long process, so read the textbook to fully understand it. But the idea here is to make our solution much easier (or at least not impossible lol) to find. An analogy I think of is integration by substitution. We have a difficult integral in terms of x, we use a substitution u=f(x), and we get an integral in terms of u that is much easier to find. Once we find this integral, we convert our answer back into x. Using this substitution gave us a "round-a-bout" way of solving an integral. Same concept with diagonalisation.
(p.s. if anything is wrong some one correct me pls)
Ok so idk if you actually want an answer, but I'm doing it to make sure I know what I'm talking about so:
You know the usual matrix equation:
Now the whole idea behind eigenvalues/eigenvectors is to move everything in straight lines as this is the easiest way to do things (just think intuitively about this).
So we want the matrix M to "move" the vector v in straight lines essentially, and so our equation should instead be in the form:
Where
Now we call
Our first objective is to find the eigenvalues (find eigenvalues first, find eigenvectors second). To do this we re-arrange the matrix equation:
Note this is the zero vector.
Also note we multiplied the scalar
Now how do we find the values of
Well we first notice something about
But by definition the eigenvector can never be the zero vector. So we make the observation:
What does this mean? Remember what we learnt about determinants. If something is not invertible, then the determinant must be zero!
So to find eigenvalues we solve:
This will always give us some polynomial of degree equal to rows and columns of M, known as the characteristic polynomial of M. This polynomial will also be in terms of
Now we have our eigenvalues, we find our eigenvectors. This is as simple as just solving the original matrix equation:
Once this is solved, we usually get a solution which is a set in terms of a parameter
Now we know the eigenvalues and eigenvectors we can do some cool things with them. For example, diagonalisation (spelling?). This is basically making it easier to evaluate certain operations on matrixes, i.e.
This is a pretty long process, so read the textbook to fully understand it. But the idea here is to make our solution much easier (or at least not impossible lol) to find. An analogy I think of is integration by substitution. We have a difficult integral in terms of x, we use a substitution u=f(x), and we get an integral in terms of u that is much easier to find. Once we find this integral, we convert our answer back into x. Using this substitution gave us a "round-a-bout" way of solving an integral. Same concept with diagonalisation.
(p.s. if anything is wrong some one correct me pls)
